Rotation as Product of Two Reflections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
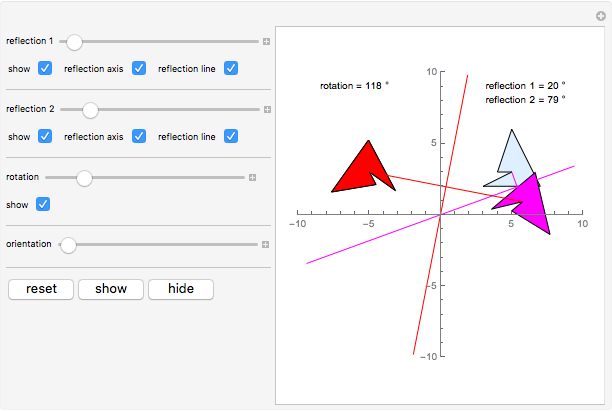
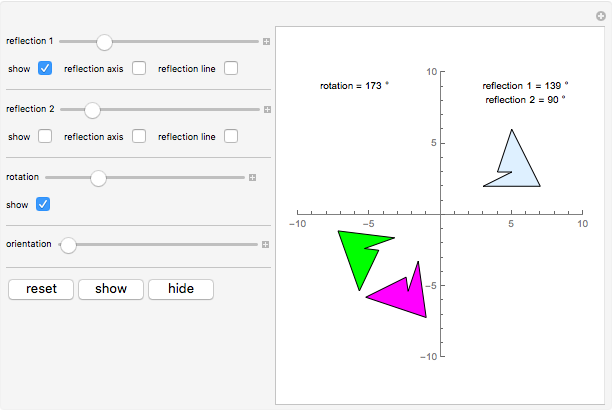
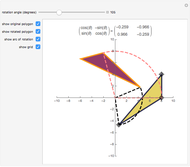
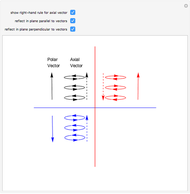
This Demonstration shows some of the relationships between composition of reflections and rotation. In particular it shows that a composition of two reflections is equivalent to a rotation. The initial graphic consists of a solid blue asymmetric object 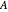 (upper right) and three translucent transforms of
(upper right) and three translucent transforms of 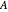 :
:
Contributed by: Ted Frazier (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
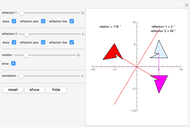
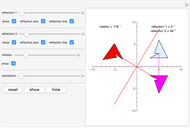
Set the "reflection 1" angle to zero. Then set the rotation to an even angle, say 118 degrees (the default). Now change the angle of "reflection 2" until the red figure is exactly over the green figure (the rotation). The reflection angle is exactly half of the rotation angle.
Snapshot 1: shows the "reflection 2" angle is half the rotation angle
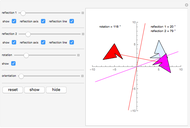
Snapshot 2: shows another pair of reflections giving the same rotation; the reflection lines have been rotated
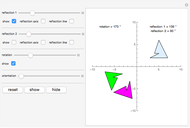
Snapshot 3: shows both reflection lines are the same; their product is the identity
With the identity (or "do nothing" transformation), reflections in lines through a point form a group 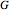 , and rotations about that point are then a subgroup of
, and rotations about that point are then a subgroup of 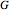 .
.
Permanent Citation