Rotation Index of Evolutes
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
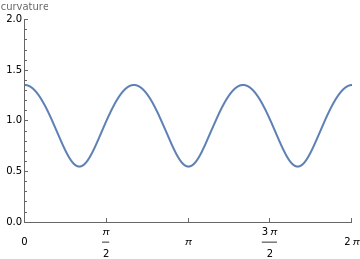
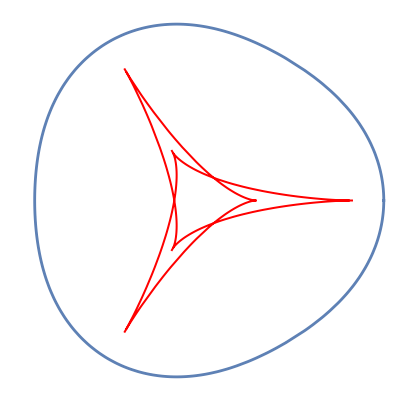
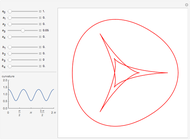
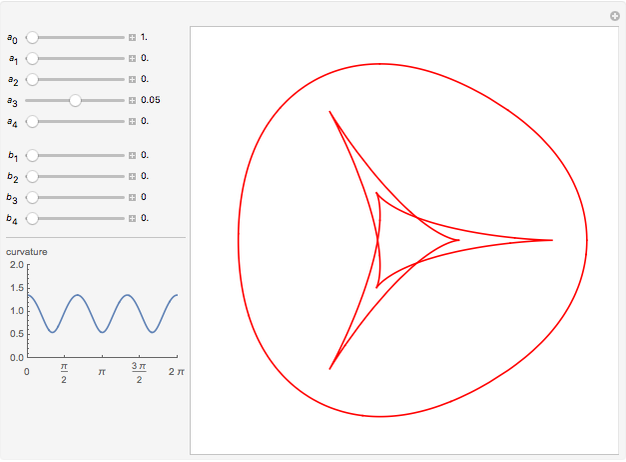
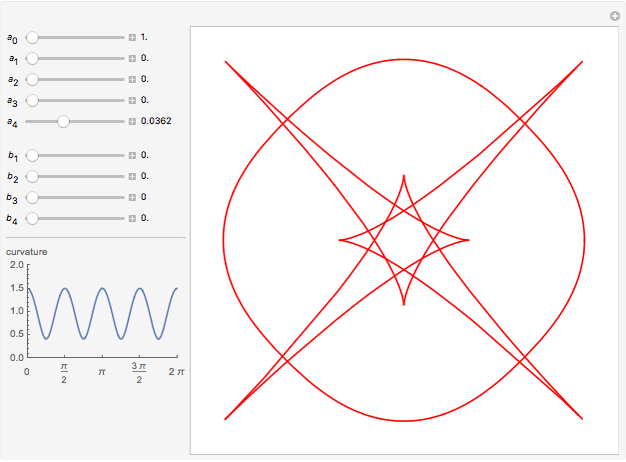
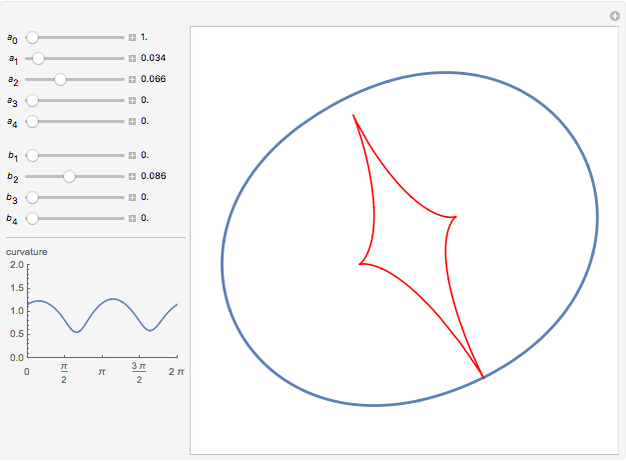
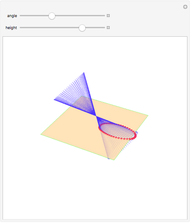
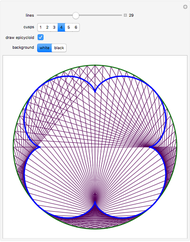
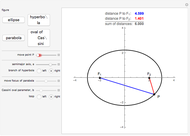
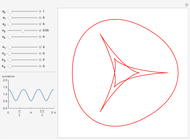
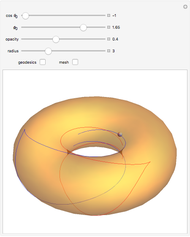
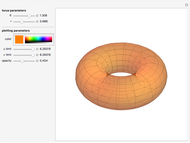
The evolute of a plane curve is the envelope of its normal lines. The evolute of a simple convex curve is closed and bounded, and its evolute has cusps corresponding to the vertices of the curve.
[more]
Contributed by: Thomas Waters (June 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] T. Waters, "The Conjugate Locus on Convex Surfaces," Geometriae Dedicata, forthcoming. arxiv.org/abs/1806.00278.
Permanent Citation