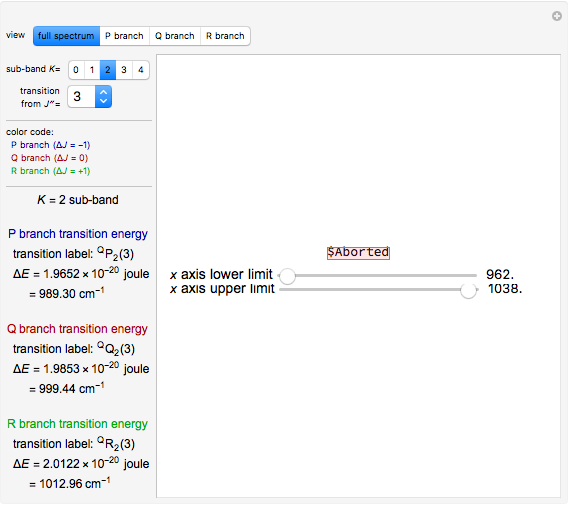
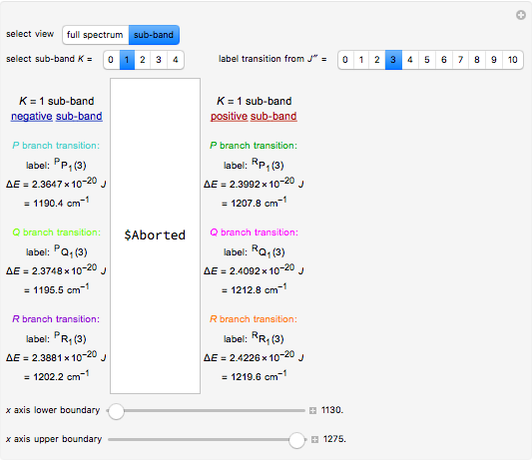
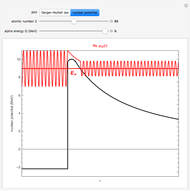
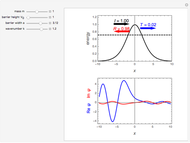
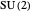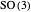Rotation of Spinors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
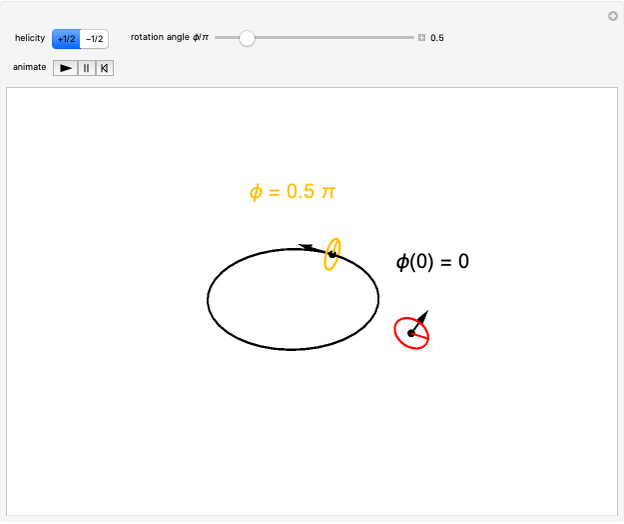
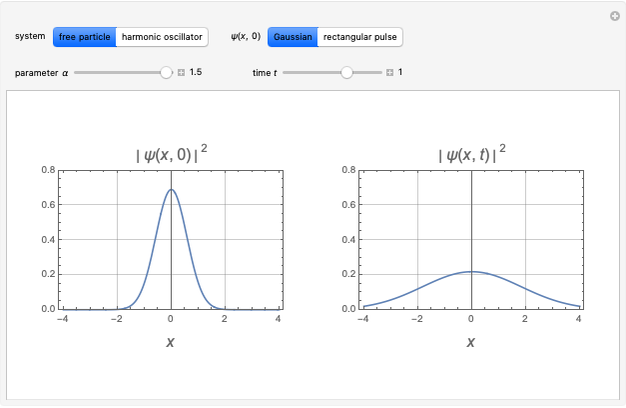
The electron, and other fermions with spin  , is described in relativistic quantum mechanics by a spinor. A distinguishing feature of spinors is their behavior under rotation. Whereas a vector boson, with spin 1, will return to its initial state after a rotation by
, is described in relativistic quantum mechanics by a spinor. A distinguishing feature of spinors is their behavior under rotation. Whereas a vector boson, with spin 1, will return to its initial state after a rotation by 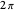 , a spinor requires two full rotations, with the angle advancing by
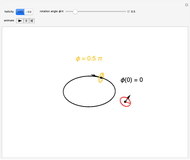
, a spinor requires two full rotations, with the angle advancing by 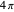 to recover its initial state. A spinor is described by a complex phasor in addition to a helicity. This is represented in the graphic by rotation in a circle normal to its spin direction, with the complex phase color coded. A rotation in space by an angle
to recover its initial state. A spinor is described by a complex phasor in addition to a helicity. This is represented in the graphic by rotation in a circle normal to its spin direction, with the complex phase color coded. A rotation in space by an angle  is accompanied by a phase change of
is accompanied by a phase change of 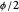 . Thus after rotation by
. Thus after rotation by  , the spin direction of the particle is recovered but the phase changes by a factor
, the spin direction of the particle is recovered but the phase changes by a factor  . This can be observed experimentally in interference phenomena, most notably those done in neutron diffraction. In the course of rotation of
. This can be observed experimentally in interference phenomena, most notably those done in neutron diffraction. In the course of rotation of  by
by 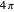 , the phasor traces out a Möbius band. This accords with the fact that a point on the surface of a Möbius band must go around twice in order to return to its initial location.
, the phasor traces out a Möbius band. This accords with the fact that a point on the surface of a Möbius band must go around twice in order to return to its initial location.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
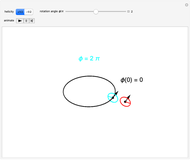
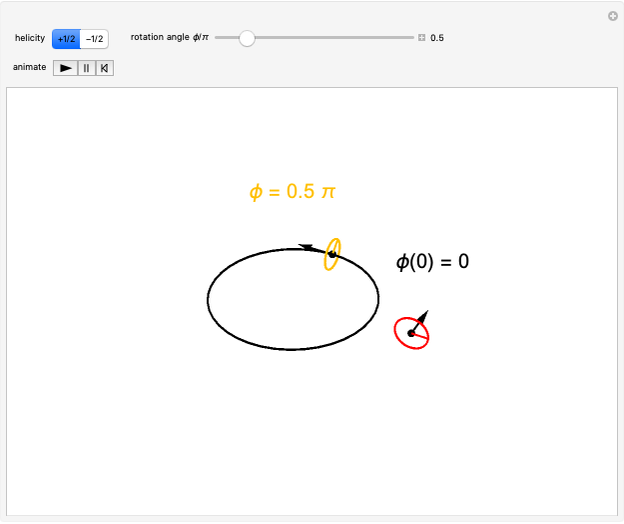
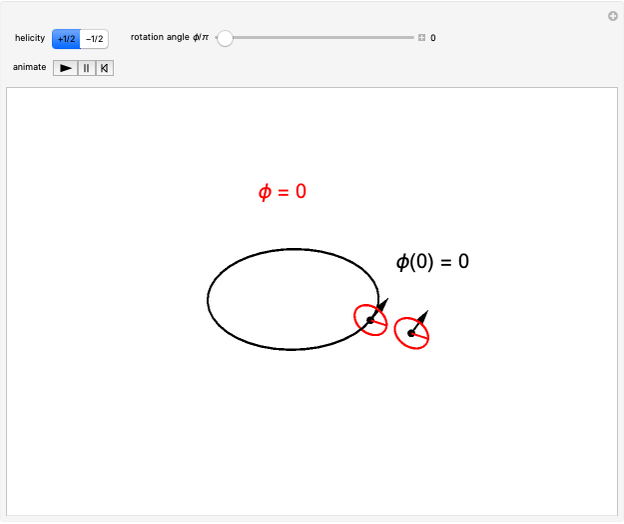
Snapshot 1: starting point
Snapshot 2: rotation by 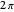 produces a phase difference of
produces a phase difference of 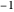
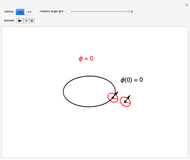
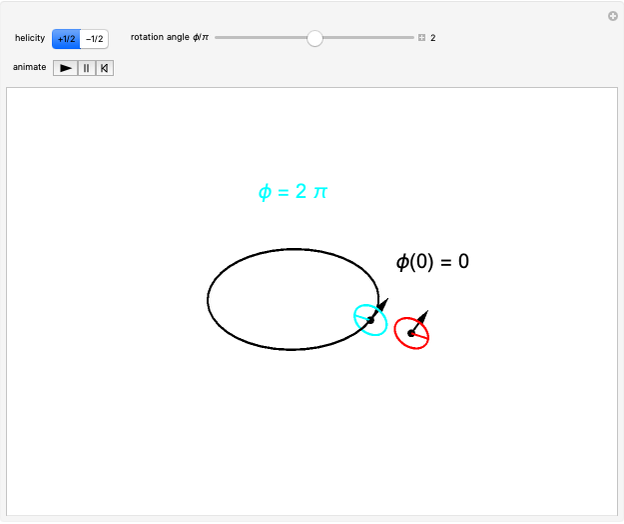
Snapshot 3: rotation by 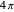 is required to recover the initial state
is required to recover the initial state
Reference
R. Penrose and W. Rindler, Spinors and Space-Time: Volume 2, Spinor and Twistor Methods in Space-Time Geometry, Cambridge: Cambridge University Press, 1988.
Permanent Citation