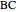Rotation of the Euler Line of a Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
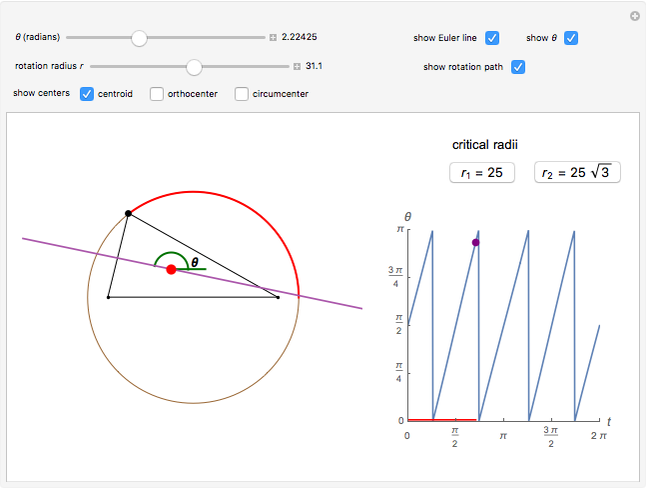
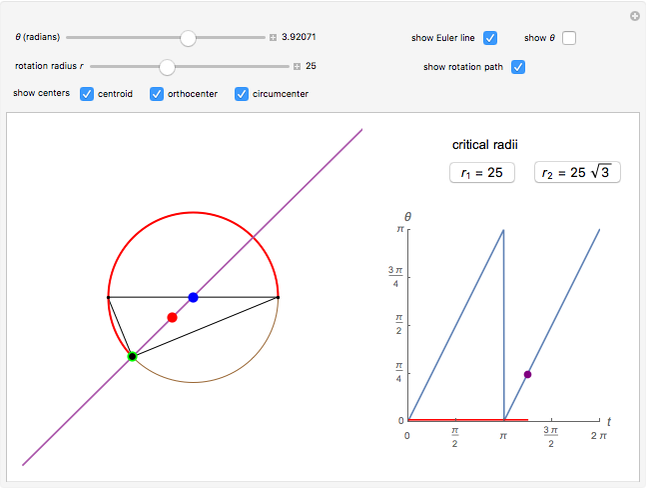
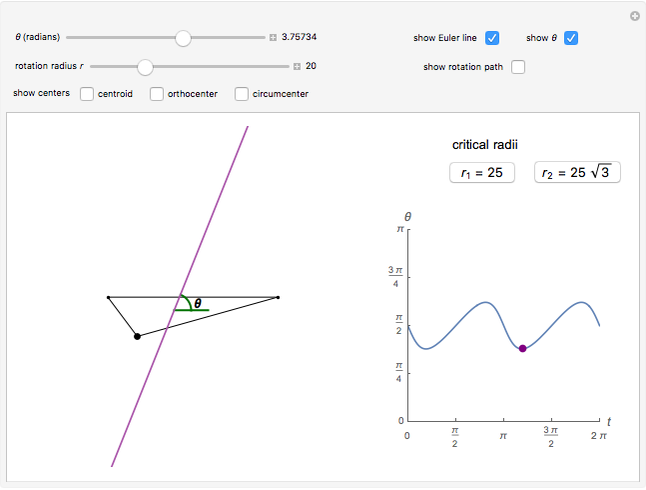
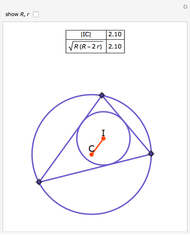
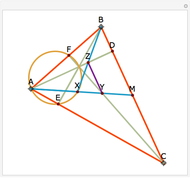
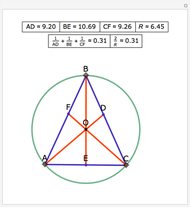
The Euler line of a triangle passes through a triangle's orthocenter, centroid and circumcenter. The orthocenter is the intersection of the three altitudes of the triangle. The centroid is the intersection of the three medians (the lines connecting each vertex to the midpoint of the opposite side). The circumcenter is the center of the circumscribed triangle.
[more]
Contributed by: Will Nute (February 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
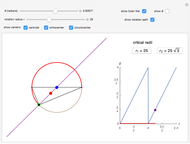
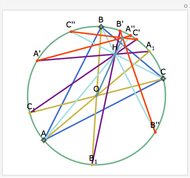
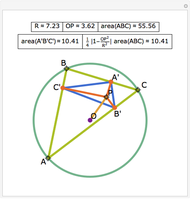
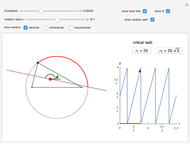
Three ranges for the circle radius produce qualitatively different results. For 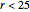 and
and 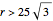 , the Euler line "wobbles" and never completes a rotation. For
, the Euler line "wobbles" and never completes a rotation. For 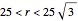 , the Euler line completes two full rotations as
, the Euler line completes two full rotations as 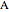 goes around the circle once. At
goes around the circle once. At 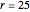 and
and  , the Euler line completes one full rotation. You can see this when the jumps on the graph (which indicate a 180° rotation) converge to two jumps instead of the four in the middle range.
, the Euler line completes one full rotation. You can see this when the jumps on the graph (which indicate a 180° rotation) converge to two jumps instead of the four in the middle range.
Torrey Pines High School, Advanced Topics in Mathematics II, 2016–2017
Permanent Citation