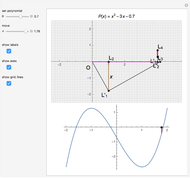
Ruffini-Horner Method for a Polynomial in Powers of x-h

Initializing live version

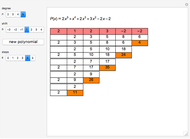
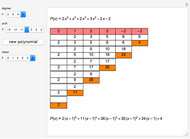
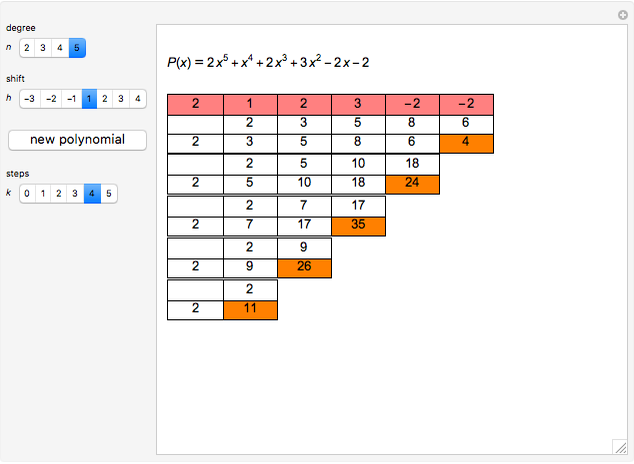
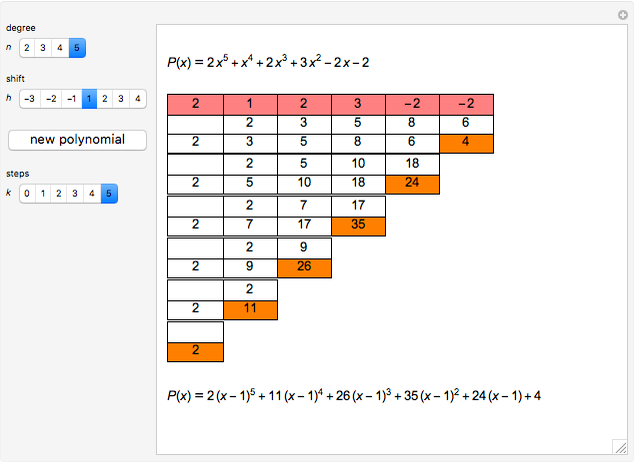
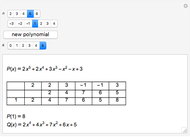
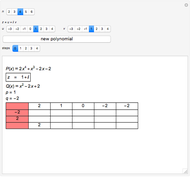
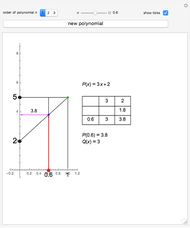
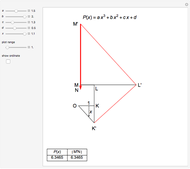
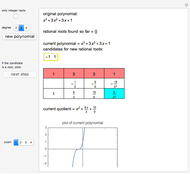
This Demonstration shows the transformation of a polynomial in powers of into a polynomial in powers of 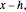using the Ruffini–Horner method.

Contributed by: Izidor Hafner (December 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Given a polynomial

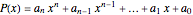find a way to express it as a polynomial in :

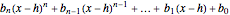One method is to use a Taylor series

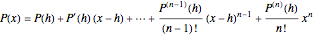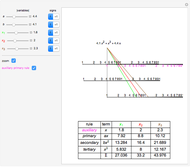
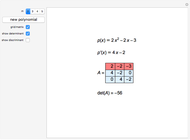
Another way is to make use of synthetic division, discovered by Ruffini in 1804 and Horner in 1819.

References

[1] Wikipedia. "Paolo Ruffini." (Dec 12, 2016) en.wikipedia.org/wiki/Paolo_Ruffini.

[2] Wikipedia. "William George Horner." (Dec 12, 2016) en.wikipedia.org/wiki/William_George_Horner.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send