Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Runge's Phenomenon

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

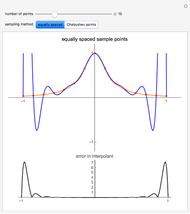
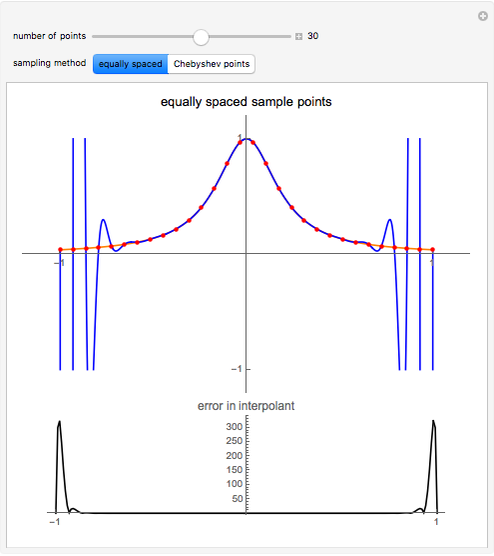
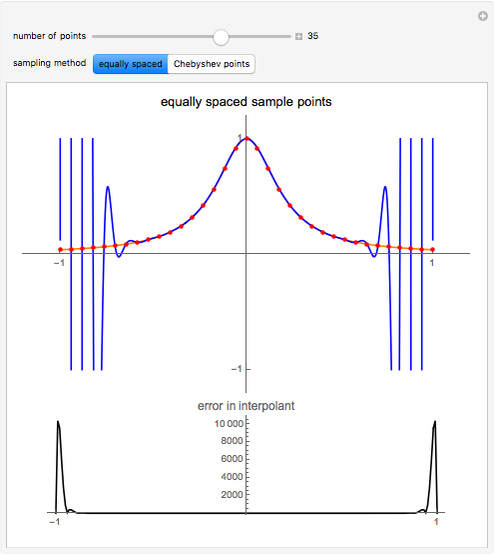
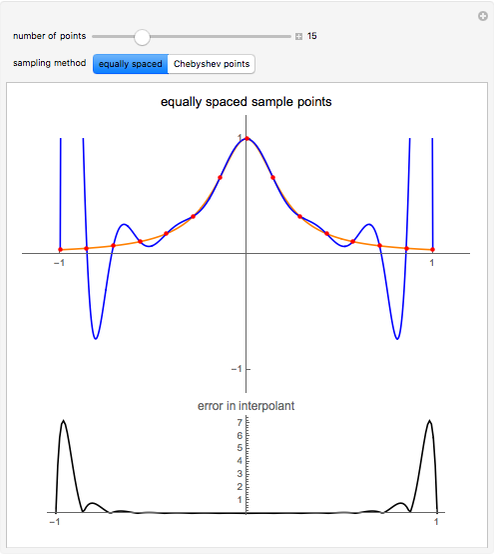
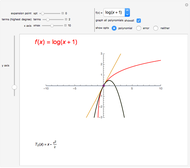
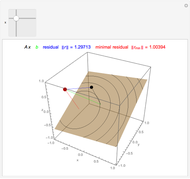
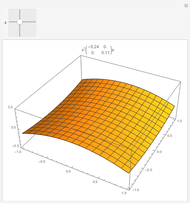
Runge's phenomenon illustrates the error that can occur when constructing a polynomial interpolant of high degree. The function to be interpolated, , is shown in orange, the interpolating polynomial in blue, and the data points in red. The difference between the interpolant and the function is shown below.

Contributed by: Chris Maes (April 2007)
Open content licensed under CC BY-NC-SA

Snapshots

Details

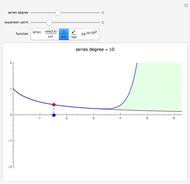
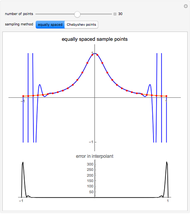
Runge's function is given by . When this function is sampled at equally spaced points in the range , as the number of sample points increase the error difference the interpolating polynomial and the function grow without bound. When Cheybshev points are used the error diminishes as the number of points increases.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send