Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Safe Operation of a Semibatch Reactor

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

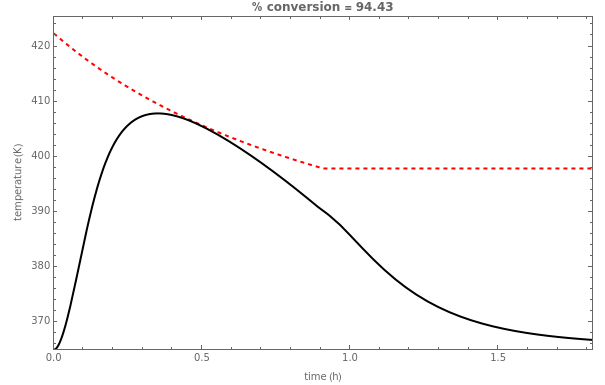
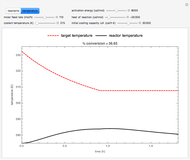
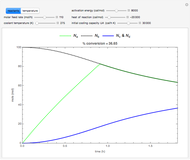
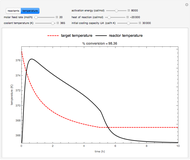
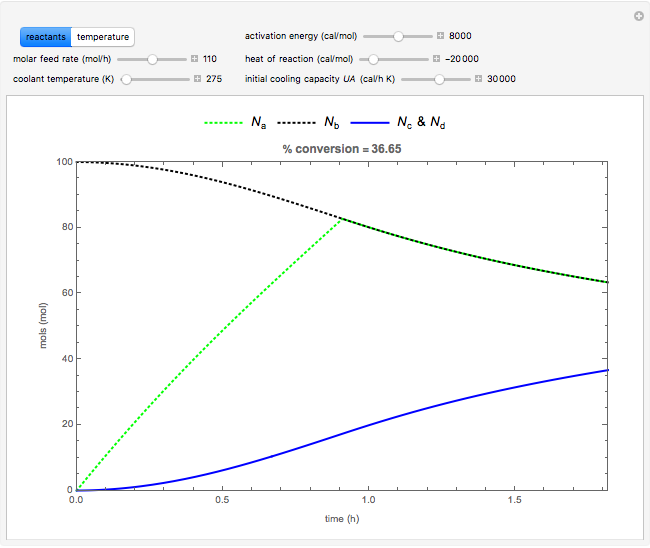
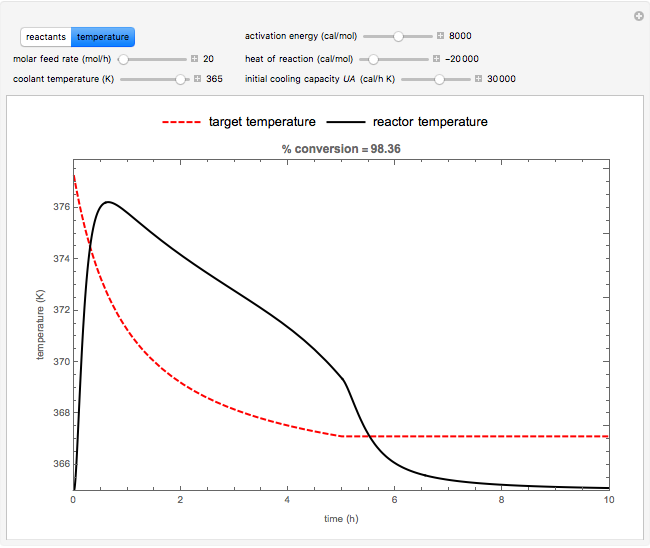
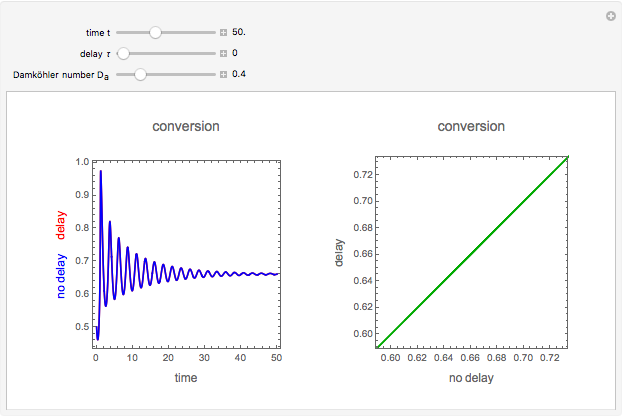
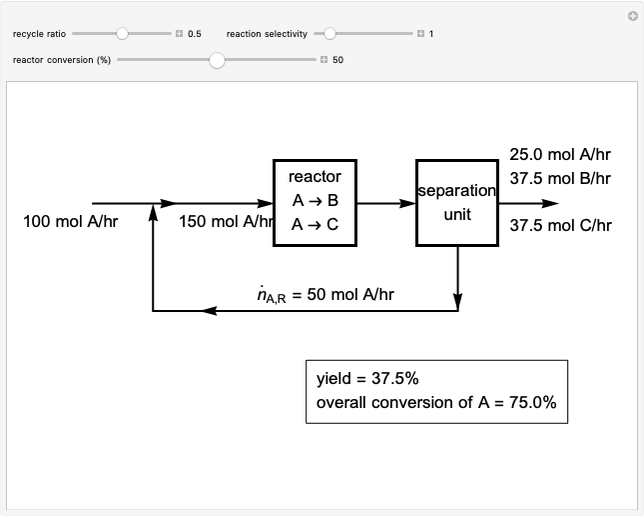
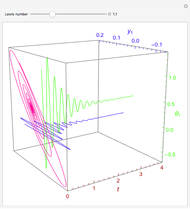
This Demonstration illustrates a method to operate a semibatch reactor to avoid thermal runaways.

[more]

2. The thermal runaway, where the reactor temperature surpasses the target temperature and approaches much higher temperatures.

3. A case in which the operating temperature is close to the maximum temperature for most of the reacting time. This results in an almost instantaneous conversion and low reactant accumulation and it is the most desirable reactor performance.

[less]

Contributed by: Clay Gruesbeck (December 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The rate law for the reaction is:

The reactant and product concentrations are:

These are the material balances:

The energy balance is:

Initial conditions for these differential equations are:

Reference

[1] K. R. Westerterp, M. Lewak, and E. J. Molga, "Boundary Diagrams Safety Criterion for Liquid Phase Homogeneous Semibatch Reactors," Industrial and Engineering Chemistry Research, 53(14), 2014 pp 5778–5791. doi:10.1021/ie500028u.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send