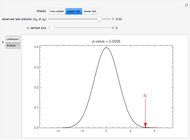
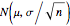Sampling Distribution of the Mean and Standard Deviation in Various Populations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
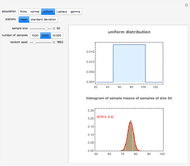
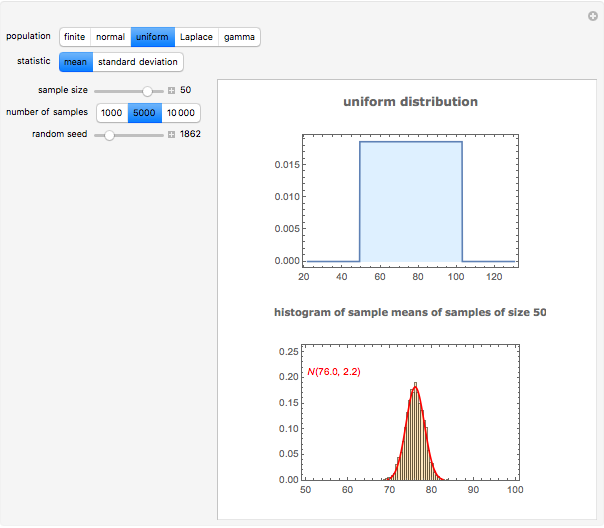
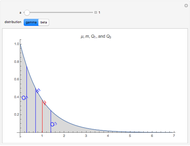
The sampling distributions for the sample mean and the sample standard deviation are explored for a finite population, as well as several infinite populations (normal, uniform, Laplace, gamma). All distributions are chosen to have the same mean, 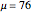 , and standard deviation,
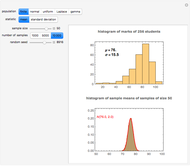
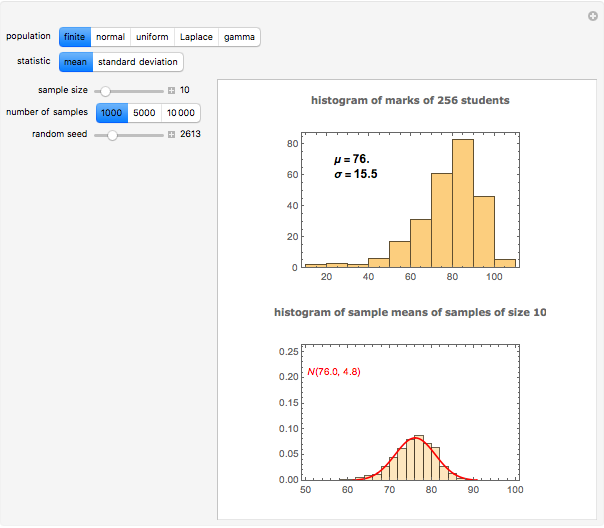
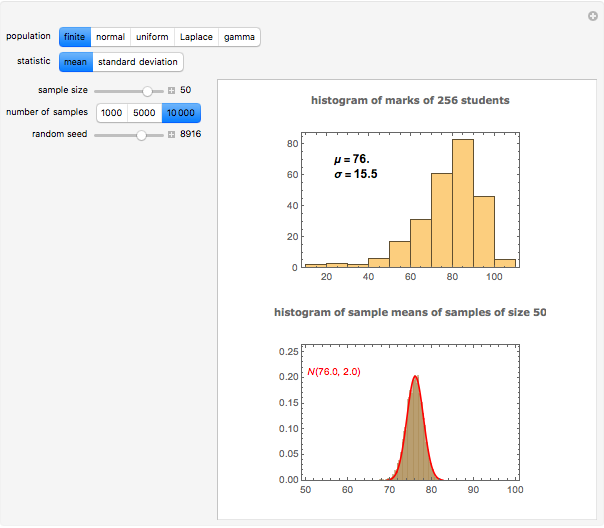
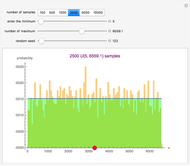
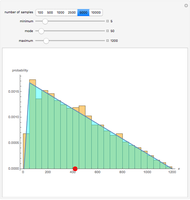
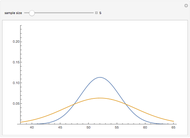
, and standard deviation, 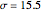 , as the finite population. The finite population consists of the marks of 256 students on a midterm test. The population distribution is shown in the top plot. The bottom plot shows normal approximation to the sampling distribution (exact for the sample mean if the population is also normal) and its empirical estimate using the histogram. These histograms are available sample sizes,
, as the finite population. The finite population consists of the marks of 256 students on a midterm test. The population distribution is shown in the top plot. The bottom plot shows normal approximation to the sampling distribution (exact for the sample mean if the population is also normal) and its empirical estimate using the histogram. These histograms are available sample sizes, 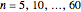 and for 1000, 5000 and 10000 samples at a time.
and for 1000, 5000 and 10000 samples at a time.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the infinite population case, the sample mean has a normal distribution with mean 76 and standard deviation 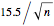 , where
, where  is the sample size.
is the sample size.
Sampling in the finite population is without replacement. In this case, the variance of the sampling distribution for the mean is adjusted by multiplying by the finite population correction factor  , where
, where  is the population size.
is the population size.
[1] I. McLeod, "Simple Random Sampling," Encyclopedia of Statistical Sciences, Vol. 12, 2nd ed. (S. Kotz, C. B. Read, N. Balakrishnan, and B. Vidakovic, eds.), New York: Wiley, 2005 p. 7740.
Permanent Citation