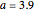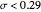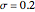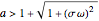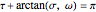Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Scalar Delay Logistic Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

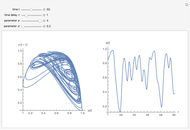
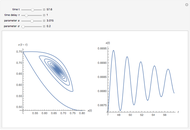
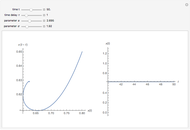
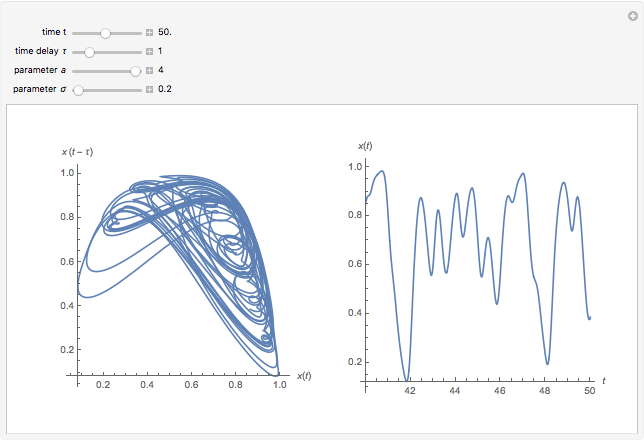
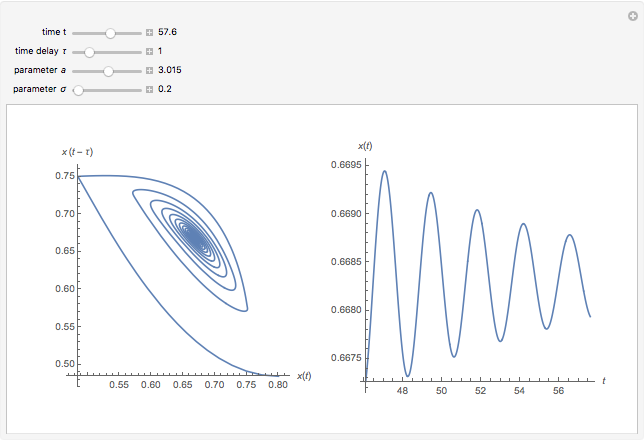
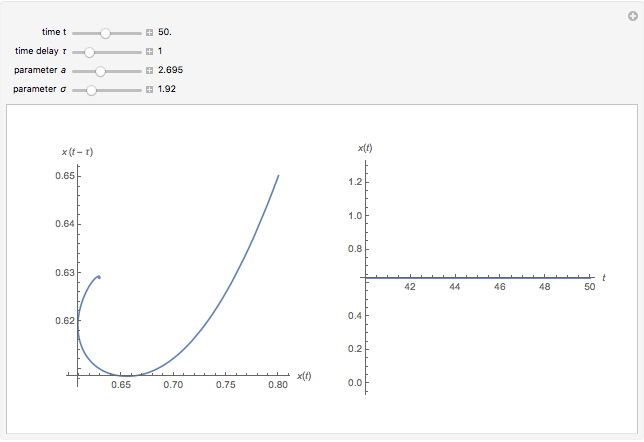
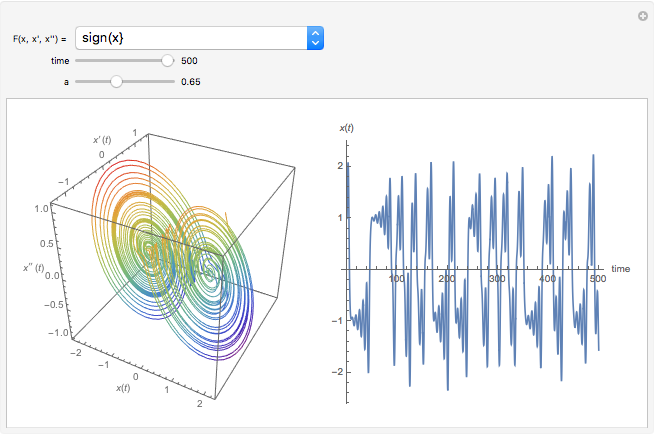
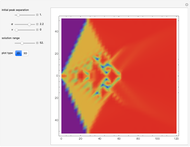
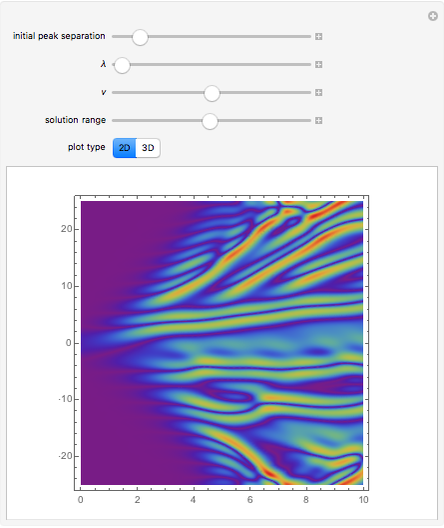
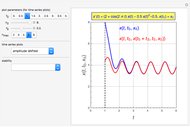
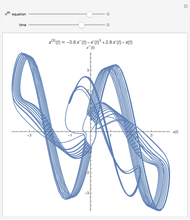
This Demonstration shows the solution of a simple scalar logistic delay equation that has found application in chemical engineering problems:

[more]

,

where is the time delay and and are positive constants. The values of the parameters generating bifurcations can be determined analytically [1]. Assuming the parameter values , , chaos occurs for approximately; for large values of all oscillations disappear. Also interesting is the effect of time delay on the generation of chaos: when and , all oscillations disappear at low values of . A necessary and sufficient condition for generating oscillations is , where the frequency is determined from the relationship .

[less]

Contributed by: Clay Gruesbeck (March 2013)
Open content licensed under CC BY-NC-SA

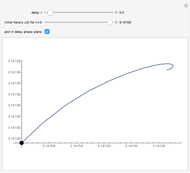
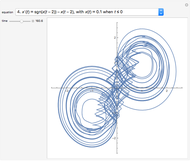
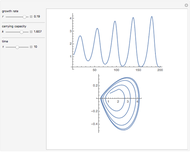
Snapshots

Details

Reference

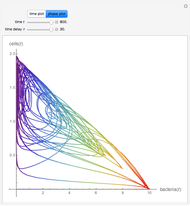
[1] M. Berezowski, "Effect of Delay Time on the Generation of Chaos in Continuous Systems. One-Dimensional Model. Two-Dimensional Model—Tubular Chemical Reactor with Recycle," Chaos, Solitons and Fractals, 12(1), 2001 pp. 83–89. doi:10.1016/S0960-0779(99)00171-X.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send