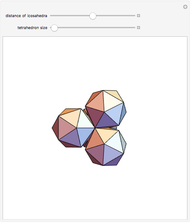
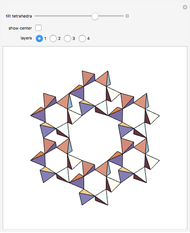
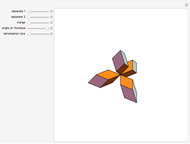
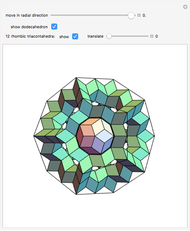
Scalenohedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
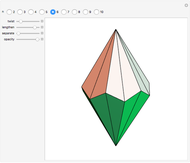
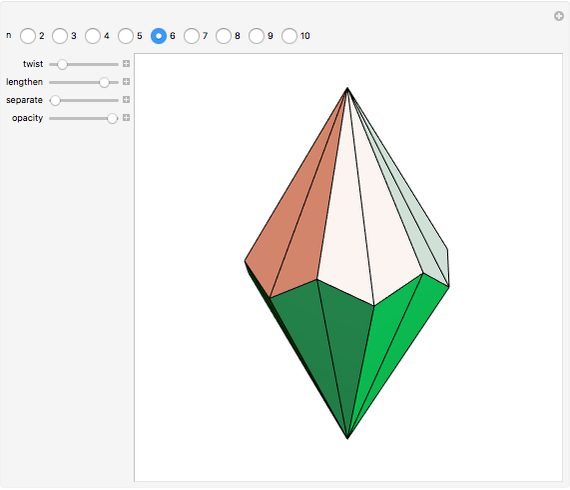
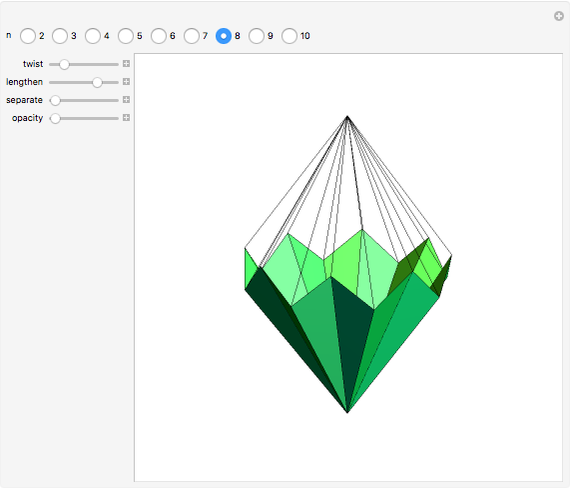
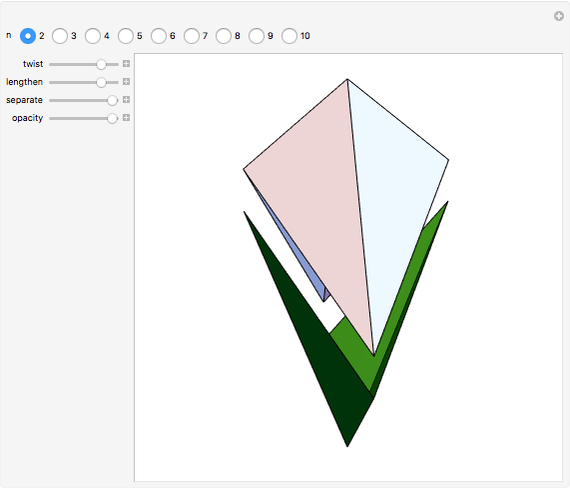
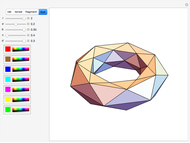
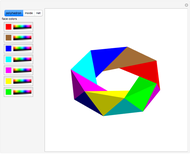
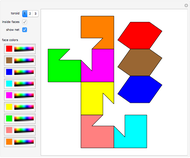
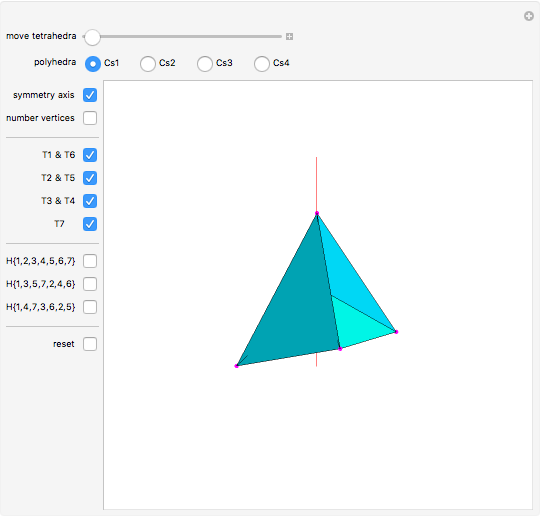
A di- -gonal scalenohedron is bounded by
-gonal scalenohedron is bounded by  mutually congruent scalene triangles. As a convex polyhedron with
mutually congruent scalene triangles. As a convex polyhedron with  and
and  , it occurs as a crystal form of certain minerals.
, it occurs as a crystal form of certain minerals.
Contributed by: Sándor Kabai, Gábor Gévay and Lajos Szilassi (July 2008)
Open content licensed under CC BY-NC-SA
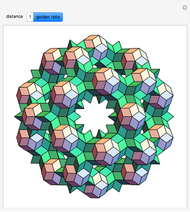
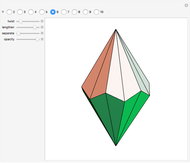
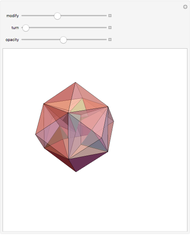
Snapshots
Details
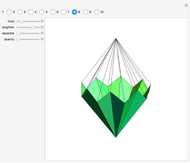
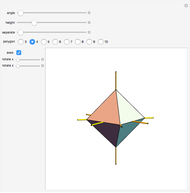
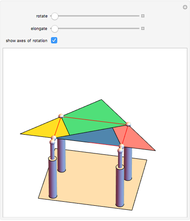
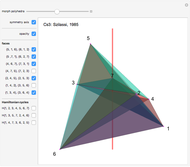
Consider a regular polygon with  sides in a horizontal plane. Raise and lower its alternate vertices to get a regular skew polygon. Take its (vertical) axis of rotation, and, for some
sides in a horizontal plane. Raise and lower its alternate vertices to get a regular skew polygon. Take its (vertical) axis of rotation, and, for some  , choose a pair of points on this axis at heights
, choose a pair of points on this axis at heights  and
and  . Take each of those points as an apex connected to the vertices of the regular skew polygon by
. Take each of those points as an apex connected to the vertices of the regular skew polygon by  edges. These edges, together with the sides of the skew polygon, form the
edges. These edges, together with the sides of the skew polygon, form the  triangular faces of a general di-
triangular faces of a general di- -gonal scalenohedron. A general di-
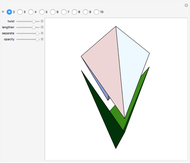
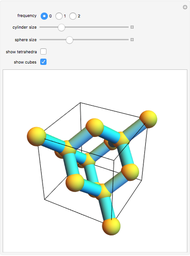
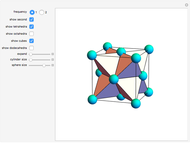
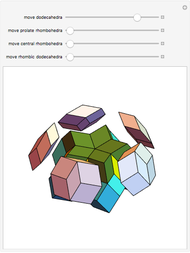
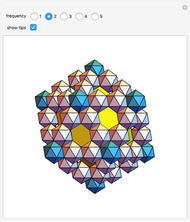
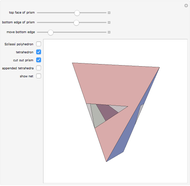
-gonal scalenohedron. A general di- -gonal scalenohedron is not necessarily a convex polyhedron. By moving the contols, you can see that in special cases bipyramids, streptohedra, rhombohedra, tetrahedra, and even the cube appear. In nature, the ditrigonal scalenohedron occurs as a well-known crystal form of calcspar (calcite). For
-gonal scalenohedron is not necessarily a convex polyhedron. By moving the contols, you can see that in special cases bipyramids, streptohedra, rhombohedra, tetrahedra, and even the cube appear. In nature, the ditrigonal scalenohedron occurs as a well-known crystal form of calcspar (calcite). For  , the name tetragonal scalenohedron is preferred for "di-digonal scalenohedron" (a crystal form of chalcopyrite, the most frequent ore of copper).
, the name tetragonal scalenohedron is preferred for "di-digonal scalenohedron" (a crystal form of chalcopyrite, the most frequent ore of copper).
Permanent Citation