Mathematica MathWorld Wolfram Science More »

HOME

TOPICS

LATEST

Schoenberg Plane-Filling Curve


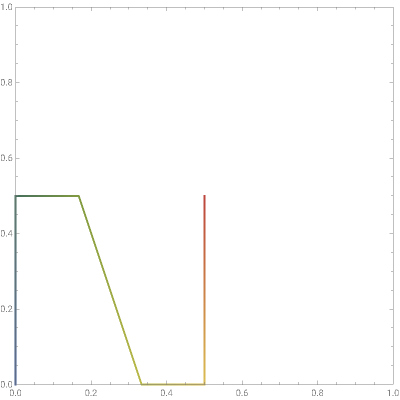
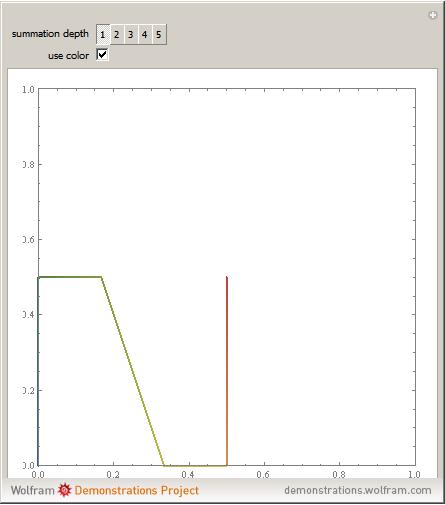
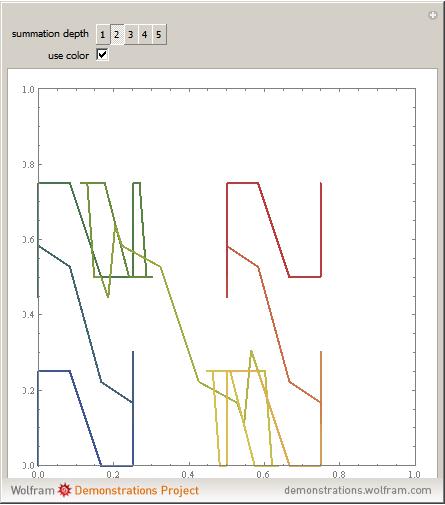
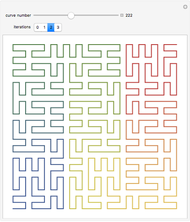
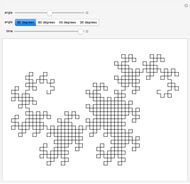
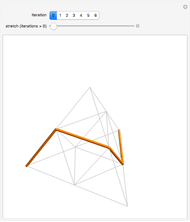
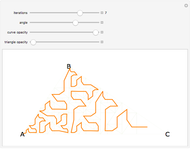
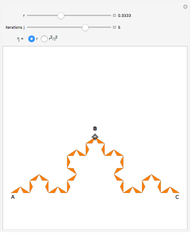
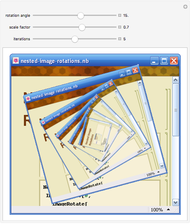
	The definition of the Schoenberg curve begins with a piecewise sawtooth-like function whose values lie between 0 and 1. The plane-filling curve is defined parametrically using sums of scaled copies of the original function. In the limit, the Schoenberg curve touches every point in the unit square.


	Contributed by: Robert Dickau
	Show Initialization Code

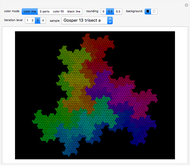
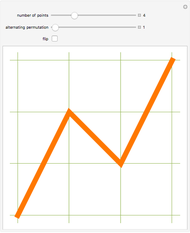
Snapshot 1: first term of the summation, the upper-right corner of which is the point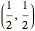

; the line color changes from blue to red to help the eye track the progress of the curve from the lower left-corner to the upper-right corner

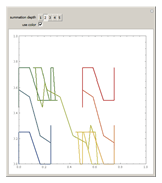
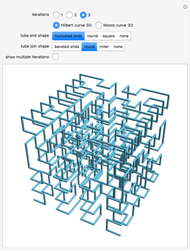
Snapshot 2: the Schoenberg curve differs from such plane-filling curves as the Peano curves, Hilbert and Moore curves, Lebesgue curve, and so forth, in that it intersects itself and indeed doubles back on itself

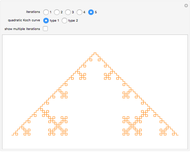
Snapshot 3: greater iterations reach more points in the unit square

I. J. Schoenberg, "On the Peano Curve of Lebesgue," I. J. Schoenberg: Selected Papers, Vol. 1 (C. de Boor, ed.), Boston: Birkhäuser, 1988.

Plane-Filling Function (Wolfram MathWorld)

"Schoenberg Plane-Filling Curve" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/SchoenbergPlaneFillingCurve/

Contributed by: Robert Dickau

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Browse all topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom