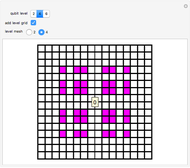
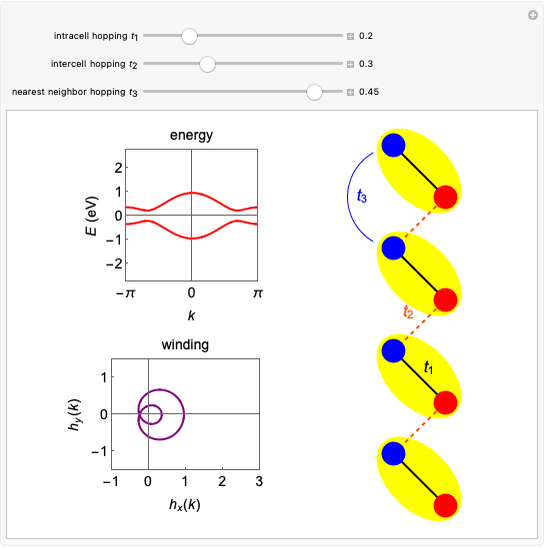
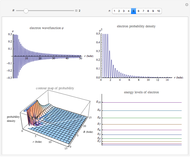
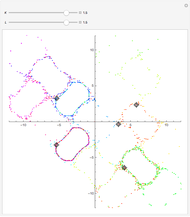
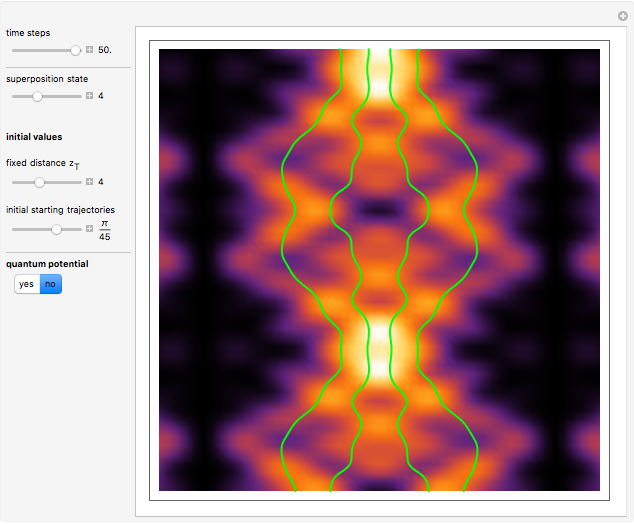
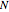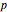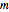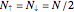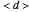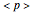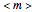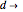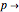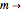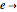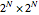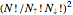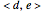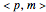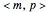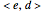This Demonstration provides a "qubistic" representation of basis states in many-body wavefunctions of quantum-mechanical Hamiltonians, such as the Hubbard model for strongly correlated electron systems.
Specifically, basis states of the half-filled Hubbard model with 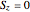 quantum number are considered. Each
quantum number are considered. Each 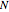 -particle state is described by the electron occupation of the
-particle state is described by the electron occupation of the 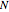 lattice sites, which can be occupied by a spin-up electron (
lattice sites, which can be occupied by a spin-up electron (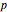 ) or a spin-down electron (
) or a spin-down electron (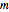 ), doubly-occupied with antiparallel spins (
), doubly-occupied with antiparallel spins ( ), or empty (
), or empty ( ). For the half-filled Hubbard model, each state has on average one electron per site and an equal number of spin-up and spin-down electrons over the
). For the half-filled Hubbard model, each state has on average one electron per site and an equal number of spin-up and spin-down electrons over the 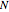 sites of the system lattice, hence
sites of the system lattice, hence 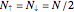 . Accordingly, the tensor basis is composed of four states
. Accordingly, the tensor basis is composed of four states 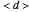 ,
, 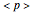 ,
, 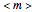 , and
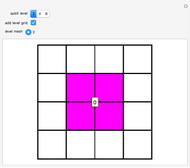
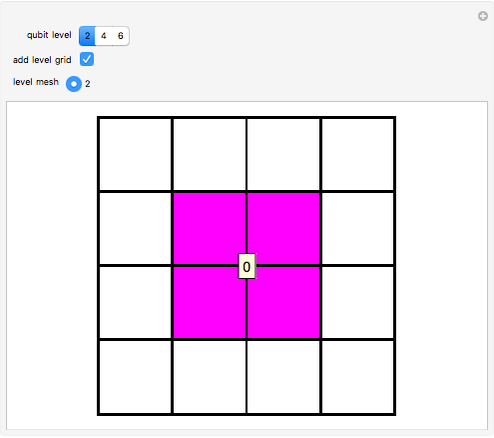
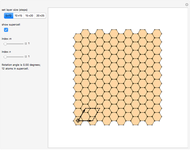
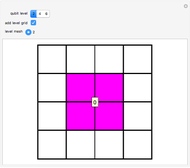
, and 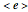 , which can in turn be associated to four level-1 squares according to the mapping:
, which can in turn be associated to four level-1 squares according to the mapping: 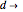 upper-left,
upper-left, 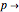 upper-right,
upper-right, 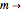 lower-left,
lower-left, 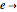 lower-right. As shown in [1], the procedure can be iterated by splitting the squares to obtain level-2 qubit representation, and so on up to the desired level-
lower-right. As shown in [1], the procedure can be iterated by splitting the squares to obtain level-2 qubit representation, and so on up to the desired level-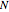 qubits.
qubits.
In general, for a given qubit level 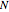 , the tensor product gives
, the tensor product gives 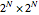 states, but states with
states, but states with 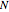 electrons and
electrons and 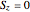 quantum number are considerably fewer, namely
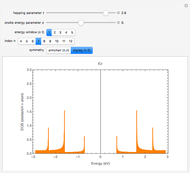
quantum number are considerably fewer, namely 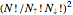 . These states are colored in the Demonstration qubistic plot, whereas states that do not have
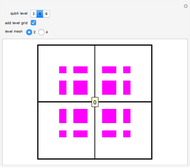
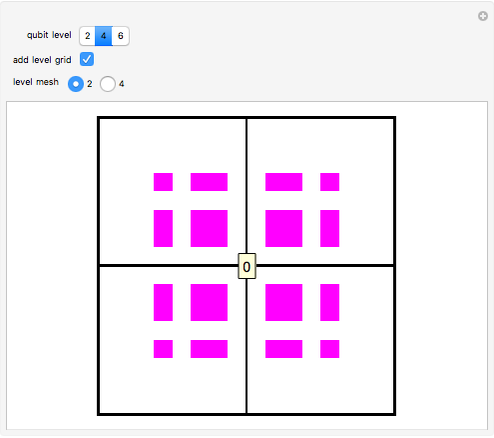
. These states are colored in the Demonstration qubistic plot, whereas states that do not have 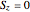 are represented by white squares and are associated with zero. For instance, level-2 colored squares map to four
are represented by white squares and are associated with zero. For instance, level-2 colored squares map to four 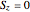 states, with an average of one electron on each of the two sites:
states, with an average of one electron on each of the two sites: 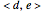 ,
, 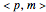 ,
, 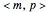 , and
, and 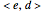 .
.
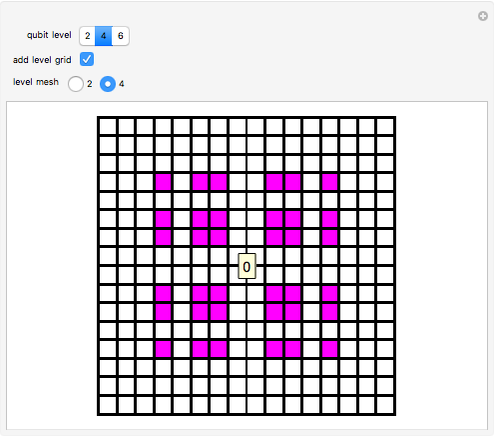
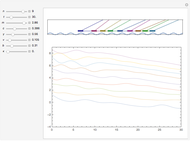
This 2D mapping displays a self-similar pattern, which shows an increasing resolution and complexity for higher 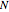 . You can verify this property by selecting the number
. You can verify this property by selecting the number 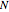 of qubits and the index related to the available sublevels mesh grids in the array plot. Moreover, by moving the mouse over the array plot you can inspect the occupation patterns of the related states and verify the presence of symmetric occupation patterns at the corners of the fractal features in the plot. Since the
of qubits and the index related to the available sublevels mesh grids in the array plot. Moreover, by moving the mouse over the array plot you can inspect the occupation patterns of the related states and verify the presence of symmetric occupation patterns at the corners of the fractal features in the plot. Since the 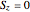 states are selected from the
states are selected from the 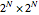 qubits, which is already huge for small
qubits, which is already huge for small 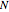 , this Demonstration is limited to level-6 qubits.
, this Demonstration is limited to level-6 qubits.
Similar visualization techniques have been applied to get a quantitative characterization of DNA and protein sequences [1].
[less]
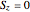 Half-Filled Hubbard Model Basis States
Half-Filled Hubbard Model Basis States