Semiclassical Quantization for Asymmetric Rigid Rotors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
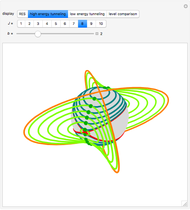
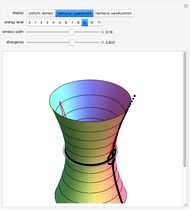
Chapter 31 of Springer Handbook of Atomic, Molecular, and Optical Physics gives a semiclassical theory of molecular rotations [1]. The primarily geometric approach produces decently accurate energy estimates from integrals along the level sets of a rotational energy surface (RES). This Demonstration works through the initial example of an asymmetric rigid rotor; however, alternative calculations and diagrams presented here rely on a more detailed theory that does not exactly follow the handbook (see Details).
Contributed by: Brad Klee (August 2019)
Open content licensed under CC BY-NC-SA
Details
Given inertial constants 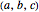 , the Hamiltonian function,
, the Hamiltonian function,
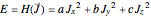 ,
,
determines the conserved energy 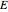 of a rigid rotor with angular momentum vector
of a rigid rotor with angular momentum vector 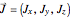 . Another constraint,
. Another constraint,
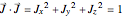 ,
,
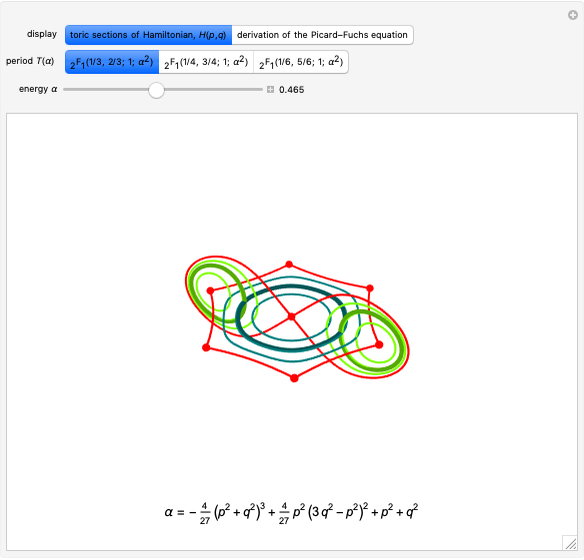
expresses conservation of angular momentum in normalized units. Assuming that both conservation laws hold indefinitely, the 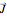 vector is constrained to remain on an algebraic sphere curve,
vector is constrained to remain on an algebraic sphere curve,
 (in blue-green).
(in blue-green).
Euler's equations for rigid-body rotation, 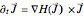 , define the natural time parameter. As time goes on, the
, define the natural time parameter. As time goes on, the  vector precesses around curve
vector precesses around curve 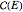 , with one complete cycle measured by period function
, with one complete cycle measured by period function 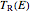 .
.
Given a division of the sphere into isoenergetic curves, a rotational energy surface can be written as union over the range of valid energies,
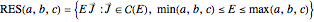 .
.
This Demonstration adopts a convention where  ,
, 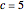 and
and  . Then all rotations fall in an energy window
. Then all rotations fall in an energy window 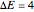 , with higher energy around the
, with higher energy around the  axis, with lower energy around the
axis, with lower energy around the 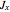 axis, and with
axis, and with 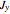 intermediate between the two extremes. Strictly speaking, the RES is not a necessity for calculation. However, it certainly helps to develop intuition. It can be plainly seen how the separatrix (in red) divides the entire surface into two double wells, one at high energy and another at low energy. To recover the curves
intermediate between the two extremes. Strictly speaking, the RES is not a necessity for calculation. However, it certainly helps to develop intuition. It can be plainly seen how the separatrix (in red) divides the entire surface into two double wells, one at high energy and another at low energy. To recover the curves 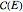 from the RES, we need only apply central projection to the surface of a unit sphere.
from the RES, we need only apply central projection to the surface of a unit sphere.
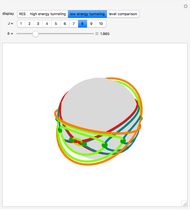
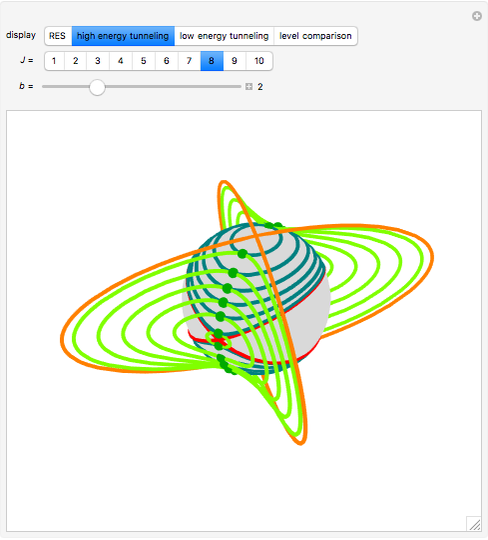
In classical mechanics, only the curves 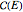 are ever necessary to determine precession motion. Quantum mechanics allows for classically forbidden tunneling motion, where the
are ever necessary to determine precession motion. Quantum mechanics allows for classically forbidden tunneling motion, where the  vector jumps between isoenergetic curves on either side of the red separatrix. The complex curves
vector jumps between isoenergetic curves on either side of the red separatrix. The complex curves
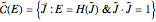 , (in green)
, (in green)
with either 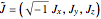 or
or 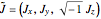 , give a geometric characterization of tunneling motion. In both cases, the second constraint
, give a geometric characterization of tunneling motion. In both cases, the second constraint 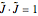 determines a circular hyperboloid, where the green tunneling curves reside. During a tunneling event, the
determines a circular hyperboloid, where the green tunneling curves reside. During a tunneling event, the  vector travels halfway around a green curve, between mirror-image teal curves. It is possible to assign a finite time to this motion, again by integrating the equations of motion. The function
vector travels halfway around a green curve, between mirror-image teal curves. It is possible to assign a finite time to this motion, again by integrating the equations of motion. The function  is used to denote the time around a complete cycle
is used to denote the time around a complete cycle 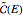 .
.
Real and complex action functions 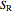 and
and 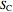 are defined directly as the solid angles interior to curves
are defined directly as the solid angles interior to curves 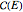 and
and 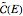 , respectively. Aside from Euler's equations, the real and complex period functions can also be calculated as first energy derivatives of the corresponding action functions, that is,
, respectively. Aside from Euler's equations, the real and complex period functions can also be calculated as first energy derivatives of the corresponding action functions, that is, 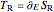 and
and 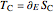 . In fact, there is another, easier way to determine the period functions.
. In fact, there is another, easier way to determine the period functions.
As in [2], dihedral symmetry allows us to derive the differential equation,
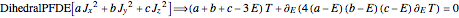 ,
,
which constrains all period integrals along the rigid-rotor RES. Two linearly independent solutions of the rigid rotor ODE can be expanded in series as
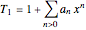 ,
,
 ,
,
with 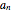 and
and  coefficients determined by Frobenius's method. Every possible solution of the period ODE, including both
coefficients determined by Frobenius's method. Every possible solution of the period ODE, including both 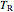 and
and 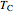 , is then a linear superposition,
, is then a linear superposition, 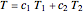 .
.
Trivially, for the real period 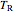 around the teal curves, we have that
around the teal curves, we have that 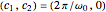 , with
, with 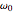 the frequency of harmonic precession,
the frequency of harmonic precession,
 .
.
The integral
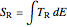
produces the real action function with 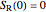 . In semiclassical quantum mechanics, the zero-order quantum energies,
. In semiclassical quantum mechanics, the zero-order quantum energies,  and
and 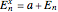 , can be calculated by root solving the stationary-phase constraint,
, can be calculated by root solving the stationary-phase constraint,
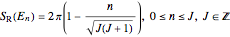 ,
,
around the high and low energy axes, respectively.
Far enough away from the red separatrix, the zero-order energy estimates do not need non-perturbative tunneling corrections. Near intermediate energy  , tunnel splitting becomes more prominent because the complex action
, tunnel splitting becomes more prominent because the complex action
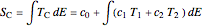 ,
,
approaches zero along with the contraction of curve 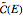 . The tunnel splitting is written as
. The tunnel splitting is written as
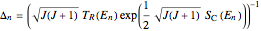 ,
,
with 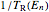 as an "attempt rate". The factor 1/2 appearing in the exponent indicates that tunneling motion only goes through half of a complete cycle. For precise evaluation of
as an "attempt rate". The factor 1/2 appearing in the exponent indicates that tunneling motion only goes through half of a complete cycle. For precise evaluation of 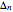 the three constants
the three constants  need to be determined. This can be accomplished by calculating no more than three numerical region integrals, as is done in the source code of this Demonstration. Once calculated, the quantities
need to be determined. This can be accomplished by calculating no more than three numerical region integrals, as is done in the source code of this Demonstration. Once calculated, the quantities 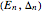 go into a tunneling matrix,
go into a tunneling matrix,
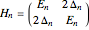 ,
,
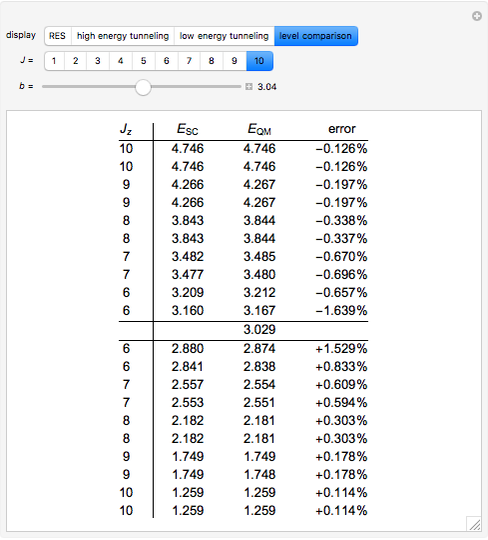
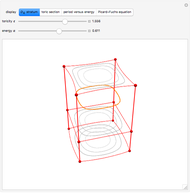
with eigenvalues 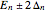 . Under the tab "level comparison", semiclassical estimates are listed in column "E(SC)" and compared to more exact matrix eigenvalues in column "E(QM)". In the final column, a percent difference is given,
. Under the tab "level comparison", semiclassical estimates are listed in column "E(SC)" and compared to more exact matrix eigenvalues in column "E(QM)". In the final column, a percent difference is given, 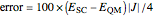 , relative to linear spacing between
, relative to linear spacing between 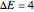 .
.
References
[1] W. G. Harter, "Molecular Symmetry and Dynamics," Springer Handbook of Atomic, Molecular, and Optical Physics (G. Drake, ed.), New York: Springer, 2006 pp. 491–513. doi:10.1007/978-0-387-26308-3_32.
[2] B. Klee. "A Few More Geometries after Ramanujan" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/AFewMoreGeometriesAfterRamanujan.
Snapshots
Permanent Citation