Sensitivity to Initial Conditions for the Logistic Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
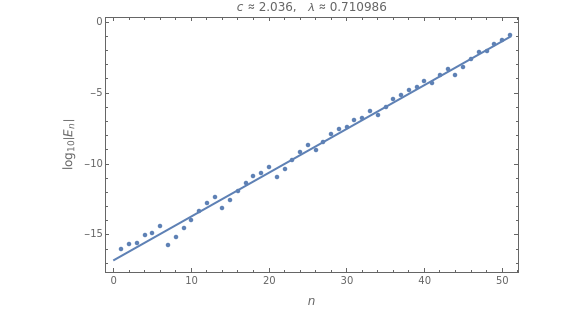
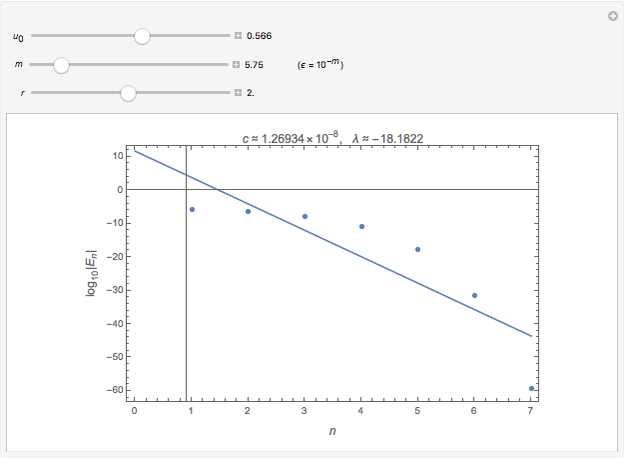
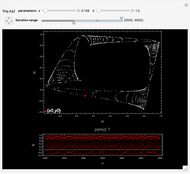
This Demonstration shows the evolution of the distance 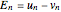 between two orbits of the logistic map
between two orbits of the logistic map  , where
, where 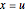 or
or  . The two orbits are initially separated by a perturbation of size
. The two orbits are initially separated by a perturbation of size  . The plot is of
. The plot is of 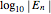 versus
versus  for an orbit starting at
for an orbit starting at  , perturbation
, perturbation  and parameter
and parameter  . An estimate of the error amplification factor
. An estimate of the error amplification factor  and the Lyapunov exponent
and the Lyapunov exponent 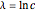 are shown at the top of the graphic.
are shown at the top of the graphic.
Contributed by: Santos Bravo Yuste (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
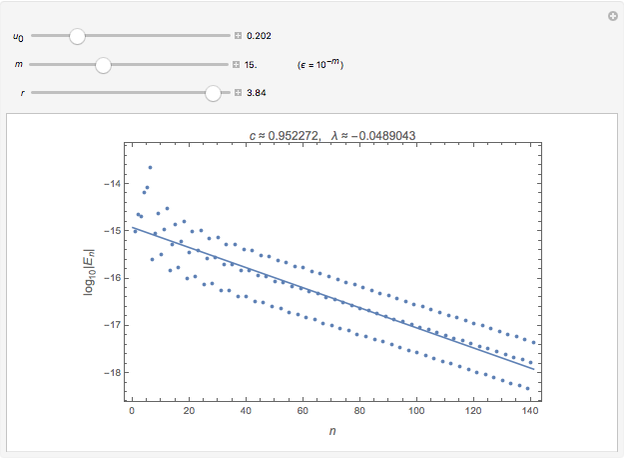
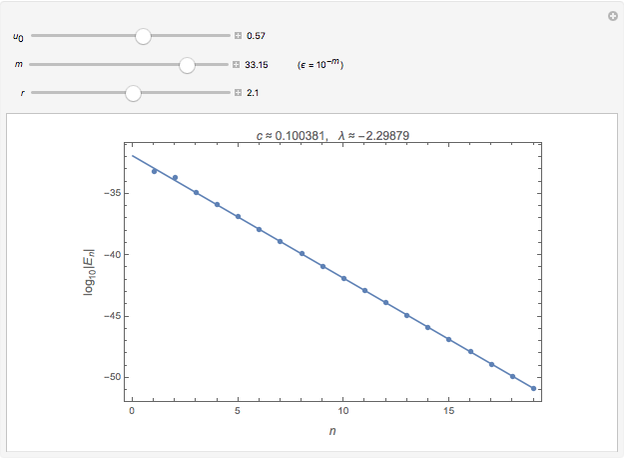
This Demonstration shows how the distance 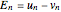 between an orbit
between an orbit 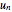 of the logistic map starting at
of the logistic map starting at  and a perturbed orbit
and a perturbed orbit  starting at
starting at  evolves. The initial perturbation
evolves. The initial perturbation  is the starting error
is the starting error 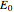 . The error changes on average with a rate
. The error changes on average with a rate  (the error amplification factor), so that the error after
(the error amplification factor), so that the error after  iterations is roughly given by
iterations is roughly given by  (see [1, Section 10.1] for more details). The Lyapunov exponent is
(see [1, Section 10.1] for more details). The Lyapunov exponent is 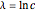 . The plot is of
. The plot is of  versus
versus  for an orbit starting at
for an orbit starting at  with perturbation
with perturbation  and parameter
and parameter  . You can explore how
. You can explore how  changes with:
changes with:
the starting value  ,
,
the initial size of the perturbation  ,
,
the parameter  of the logistic map:
of the logistic map: 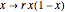 .
.
The Lyapunov exponent  is estimated by means of the slope
is estimated by means of the slope  of the linear fitting of
of the linear fitting of  . The expansion factor is
. The expansion factor is  , and
, and 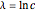 . (This exponent
. (This exponent  is better estimated by
is better estimated by 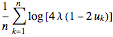 for
for 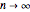 ; see the Related Link "Lyapunov Exponents for the Logistic Map" and [1]).
; see the Related Link "Lyapunov Exponents for the Logistic Map" and [1]).
The iterations stop if  or
or  or
or 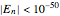 . The starting point of the perturbed orbit is
. The starting point of the perturbed orbit is  if
if  .
.
Reference
[1] H.-O. Peitgen, H. Jürgens and D. Saupe, Chaos and Fractals: New Frontiers of Science, 2nd ed., New York: Springer, 2004.
Permanent Citation