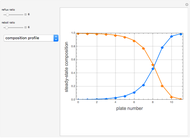
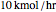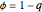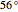Separating a Ternary Mixture of Water, 2-Propanol, and Acetone at Atmospheric Pressure

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
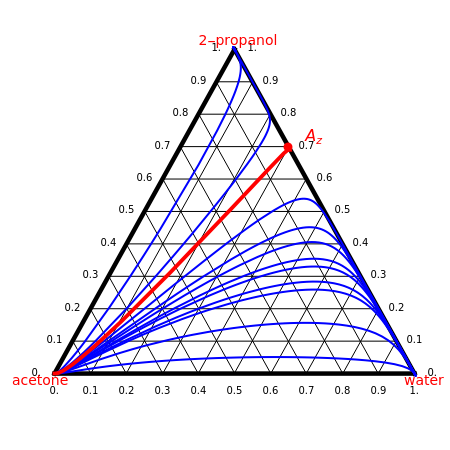
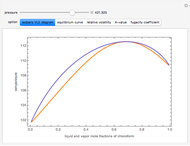
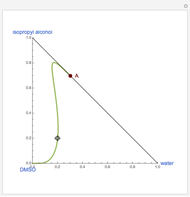
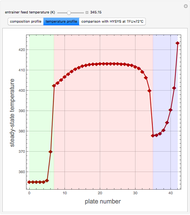
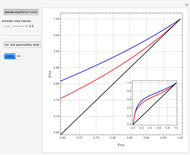
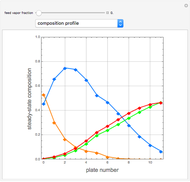
Consider a ternary mixture composed of water,  -propanol, and acetone at
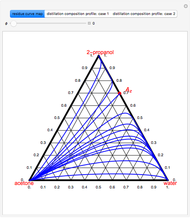
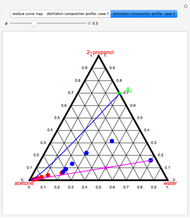
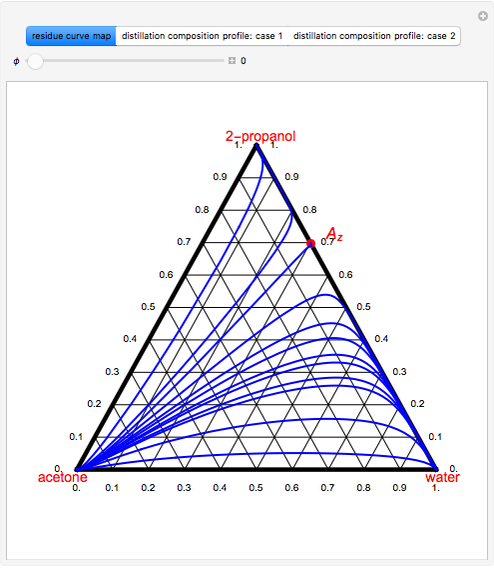
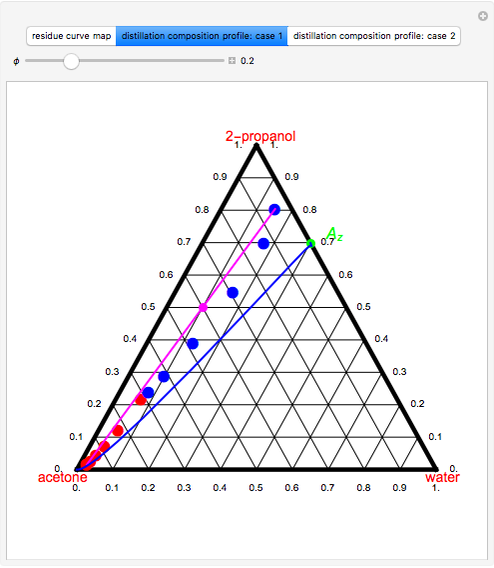
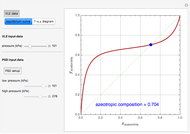
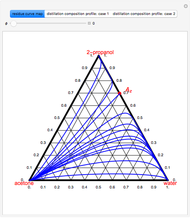
-propanol, and acetone at 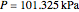 . This Demonstration plots the residue curve map (RCM) for this mixture. There are two distillation regions separated by a distillation boundary (shown in red) running from pure acetone to the only azeotrope in the ternary system (i.e., the binary azeotrope between water and
. This Demonstration plots the residue curve map (RCM) for this mixture. There are two distillation regions separated by a distillation boundary (shown in red) running from pure acetone to the only azeotrope in the ternary system (i.e., the binary azeotrope between water and  -propanol shown in red).
-propanol shown in red).
Contributed by: Housam Binous and Naim Faqir (May 2012)
Open content licensed under CC BY-NC-SA
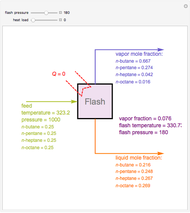
Snapshots
Details
Reference
[1] E. J. Henley and J. D. Seader, Equilibrium-Stage Separation Operations in Chemical Engineering, New York: Wiley, 1981.
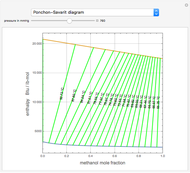
Expressions for pure component vapor and liquid enthalpies were adapted from Aspen-HYSYS. Enthalpies are in 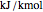 .
.
Permanent Citation