Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Separation of Topological Singularities

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

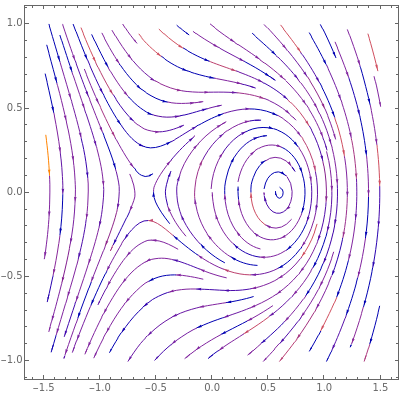
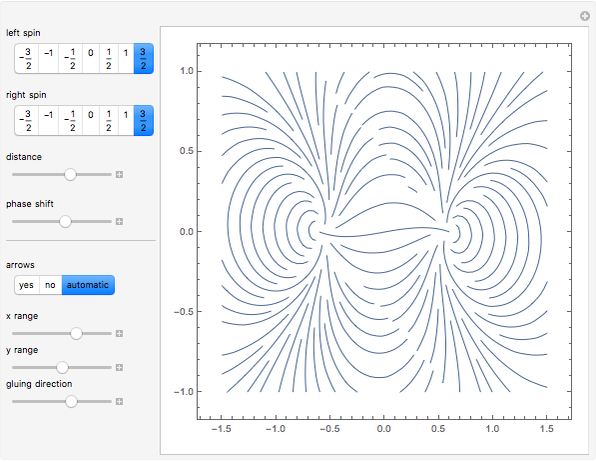
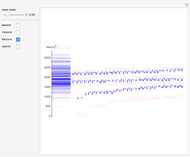
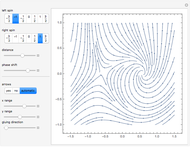
When considering nearly continuous fields of nonzero vectors in a 2D plane, there are possibly some nontrivial topological situations with enforced discontinuities at some discrete set of points. If we make a loop around one of these so-called critical points, the phase makes some integer number of rotations. Such a number has good conservation properties—the number of rotations while going through some loop is the sum of such numbers for critical points inside it. In complex analysis this is called the argument principle, in differential equations theory this number is called the Conley (or Morse) index, and in physics it is very similar to the so-called spin—while rotating around the spin axis of a particle, the quantum phase rotates times, where is the spin.

[more]

This Demonstration helps you to imagine the behavior of the phase while separating two critical points, as in the case of the spontaneous creation of a particle-antiparticle pair. It uses a very simple complex function, showing only a qualitative picture. To handle spins having a multiplicity of 1/2 as in physics, we have to identify vectors with their opposites—forget about the arrows— by using a field of directions .

[less]

Contributed by: Jarek Duda (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The function used is a slightly modified version of the complex function .

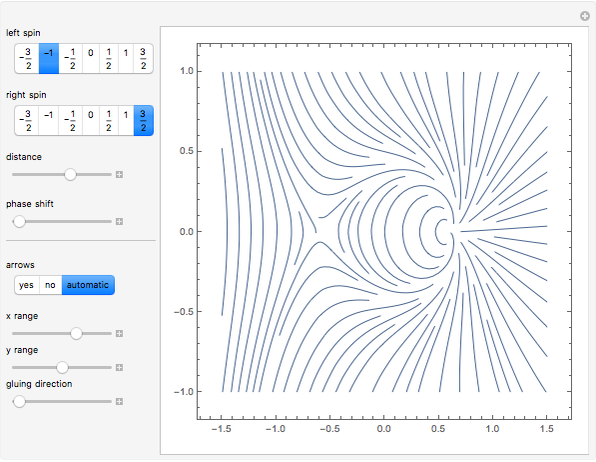
You can use the controls for either spin, the distance , the phase shift, and the magnitude. If both spins are integers, they can be used for a directed vector field. In other cases the square root produces discontinuities that vanish when we use undirected vectors. These gluings of opposite directions are visible on the plot, and their direction can be changed with the last slider.

The built-in Mathematica function StreamPlot was used so that vector lengths are suppressed to make the picture clearer.

Spin conservation can be seen in that qualitative behavior around both points does not change with distance.

This idea of constructing particles as topological singularities is expanded in the fourth section of Four-dimensional understanding of quantum mechanics.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send