Sequence Sums that are Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
With 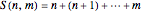 we can ask for which
we can ask for which  and
and 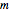 is
is  a square.
a square.
Contributed by: Karl Scherer (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
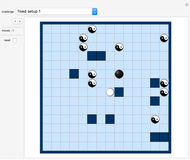
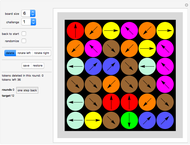
The Demonstration shows the table that lists all sequential sums  , where
, where  and
and 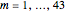 , n <= m.
, n <= m.
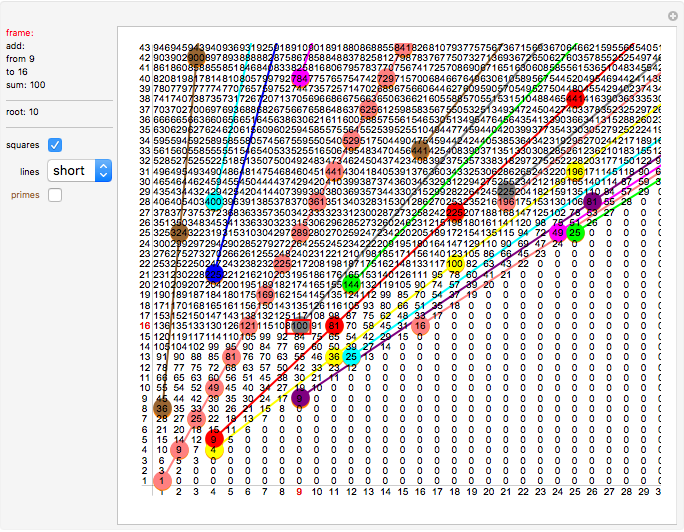
The sums that are squares are colored orange. You might see right away that several square entries are lined up on a straight line of - or so it seems - infinite length. Select "short" from the "lines" popup menu to see all lines.
Two lines in detail
Pink line: starts at {2,4} with increment {1,3}
The pink square entries covered are 9, 25, 81,...
This suggests (without formal proof) that the associated sums S(m, 3 m-2) are a square for 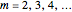 . It is easy to prove by induction that indeed we have
. It is easy to prove by induction that indeed we have
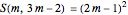 , (1),
which is a surprisingly simple formula.
In the table, the cases associated with equation (1) are connected by a straight line.
, (1),
which is a surprisingly simple formula.
In the table, the cases associated with equation (1) are connected by a straight line.
Green line: starts at {1,8} with increment {1,17}
The green square entries covered are 36, 324, 900,...
The entries highlighted by green dots suggest that 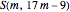 is a square for
is a square for 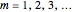 . It is easy to prove by induction that indeed we have
. It is easy to prove by induction that indeed we have
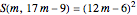 . (2)
. (2)
More lines
Altogether there are eleven lines shown in the graph:
Start pos. sum Increment {x,y} that leads to the next square
--------------------------------------------------------------------------------------
{1,1} 1 {1,3} {1,8} 36 {1,17} {4,4} 4 {7,9} {4,5} 9 {7,11} {4,21} 225 {7,43} {9,9} 9 {17,19} {9,16} 100 {17,33} {12,13} 25 {23,27} {12,20} 144 {23,41} {16,16} 16 {31,33} {24,25} 49 {47,51}
We give an example of how to read this table:
At position x=4, y=21 an entry with the sum 225 can be found . The next square in the (red) line is 7 steps to the right and 43 steps up, leading to the entry at {11, 64}. This entry carries the sum 2025, calculated from S(n,m)=(m*m + m - n*n +n)/2, which is indeed a square: 2025 = 45*45.
Can you find the associated increments of the other nine lines? Can you prove for these other nine lines that the associated (infinitely many) sums are all squares? Can you find the associated increments some line that are not shown?
Observations
Looking at the graph the following conjectures come to mind:
Observation 1: EVERY sum S(n,m) that is a square seems to lie on one of such a line.
Observation 2: No two lines cross (as long they are not extended to the left). If they are extended to the left, they seem to all intersect at the same point, namely at {.5,-.5}.
Also, it might be interesting to find out whether there is an easy way to calculate the increments from the starting values.
It is time to put the lines data into one mathematical theorem:
Without being able to prove it, the author suggests that the following is true:
Conjectured theorem
Let n and m be are natural numbers, n <= m. Let the sequential sum S(n,m) = n + ... + m be a square. Then there exist natural numbers p and q such that S(n + ip,m + iq) is square for all i=1,2,3,... Furthermore, in the set of pairs {p,q} no two elements are the same.
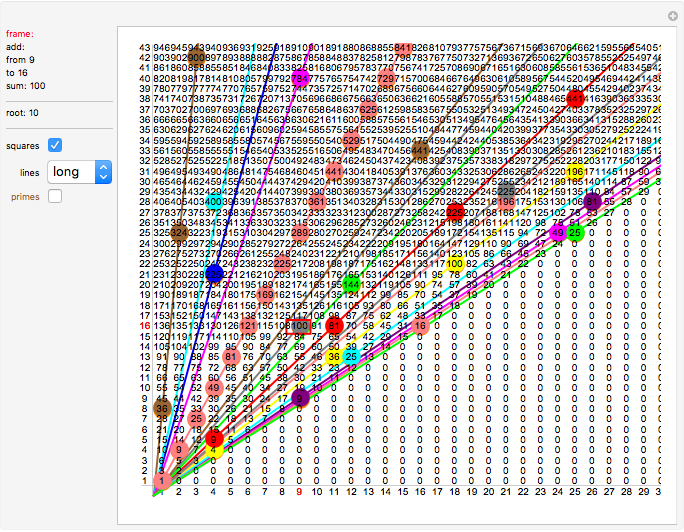
All lines intersect at {0.5,-0.5}. If P,Q are the first squares on a line, then in vector calculus we have Q-P=2*(P-{.5,-.5}). This means that the distance between two consecutive squares on a line is exactly twice the distance between the first square in a line and the intersection point {.5,-.5}.
Each line contains only one (infinite) set of regularly spaced squares.
Prime Numbers
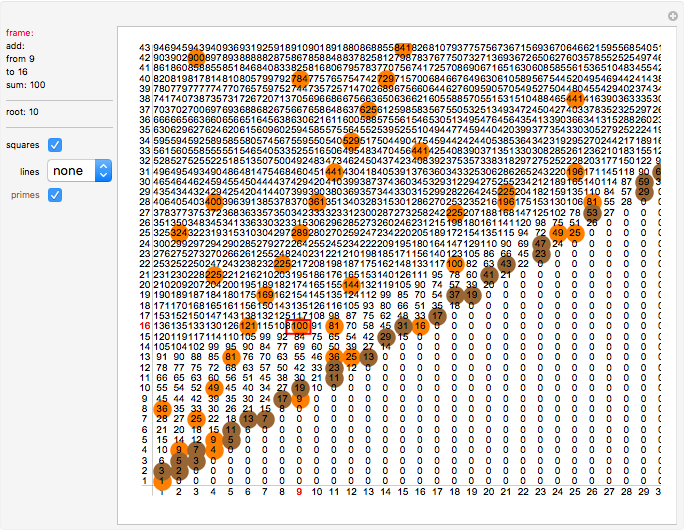
Click "primes".
The brown points mark all prime numbers in the diagram.
We see that prime numbers only occur in the main diagonal and in the next diagonal above it, but nowhere else.
Can you proof that the are no prime numbers above the second diagonal?
Well, here is the proof:
Let's assume that s = n + (n +1 ) + (n + 2) + ...+ (n + m) is a prime, with m>0.
Then s =n * (m+1) + (1 + 2 + 3 + ... + m) = n * (m+1) + (m + 1) * m/2
If m is even, then m/2 is an integer; hence k = m + 1 is odd and must be a proper divisor of s.
If m is odd, then k = (m + 1)/2 is an integer that divides s. This k is a proper divisor of s if k > 1, hence if and only if m > 1.
Hence in our table prime numbers can only occur for m = 0 or m = 1, i.e. in the main diagonal or in the one above it.
Note:
Looking at the table, you might also notice that each prime number occurs in each of the first two diagonals exactly once!
Can you see why?
Controls
Click any table entry to place a small red frame. The values of  (from) and
(from) and 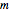 (to) associated with the clicked sum
(to) associated with the clicked sum  is displayed at the left border. If the table entry is a square, its root will also be displayed at the left border.
is displayed at the left border. If the table entry is a square, its root will also be displayed at the left border.
Click "squares" to show all squares in the table.
Setter bar "lines none/short/long": to hide/show the lines connecting an infinite number of squares each.
"Short" lines start from a square; option "long" will show the lines starting from the intersection point at {.5,-.5}.
Click "primes": to show all prime numbers in the table.
Permanent Citation