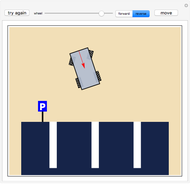
Shortest Path for the Dubins Car

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In 1957, Lester Eli Dubins proved that the shortest path between two 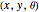 coordinates for a forward-moving vehicle with a minimum turning radius
coordinates for a forward-moving vehicle with a minimum turning radius 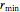 is composed entirely of no more than three circular arcs of radius
is composed entirely of no more than three circular arcs of radius 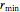 or straight lines.
or straight lines.
Contributed by: Aaron T. Becker and Shiva Shahrokhi (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
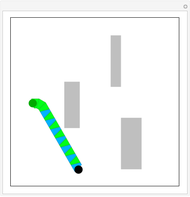
The Dubins car is a simplified mathematical model of a car that moves in the  -
-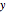 plane [1]. The car's location is specified by the
plane [1]. The car's location is specified by the 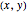 location of the center of the car's rear axle and the orientation
location of the center of the car's rear axle and the orientation  of the car. The car cannot move sideways because the rear wheels would have to slide instead of roll. The Dubins car model stipulates that the car moves forward at a constant speed and has a maximum steering angle that translates into a minimum turning radius
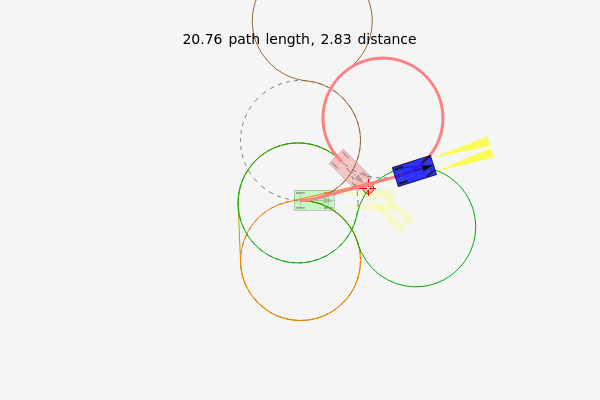
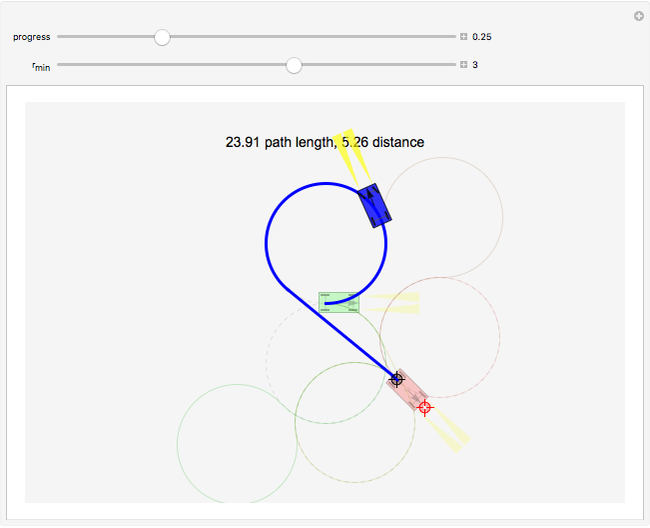
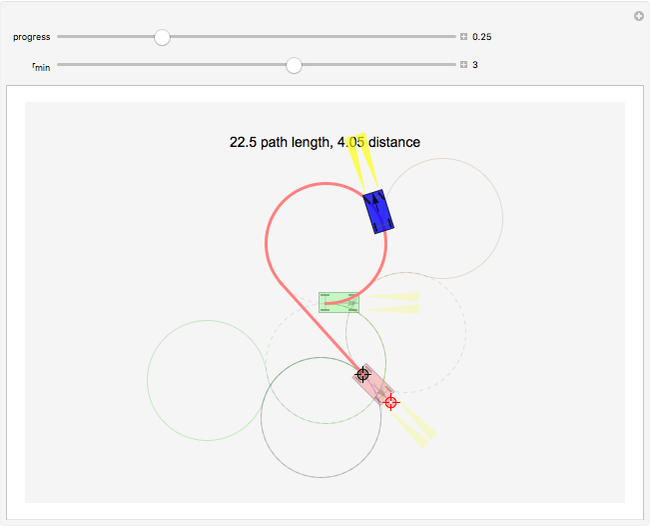
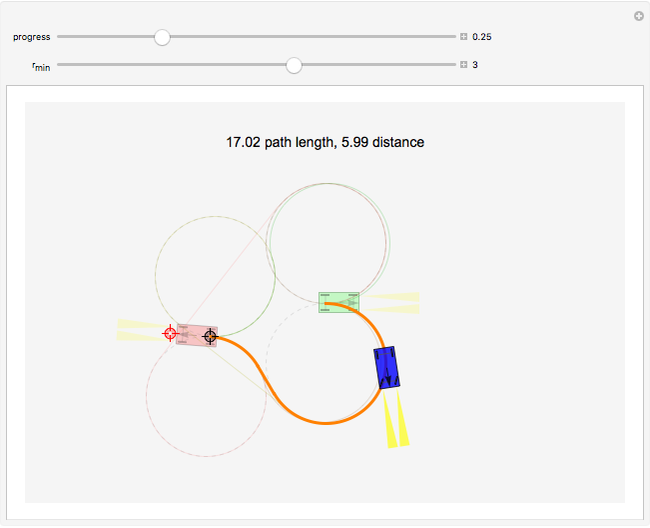
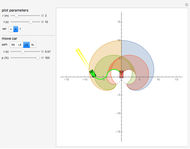
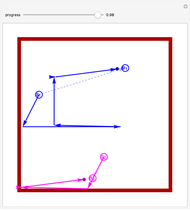
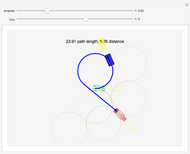
of the car. The car cannot move sideways because the rear wheels would have to slide instead of roll. The Dubins car model stipulates that the car moves forward at a constant speed and has a maximum steering angle that translates into a minimum turning radius 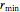 . The minimum turning radius circles are drawn tangent to the starting and ending positions with dashed gray circles.
. The minimum turning radius circles are drawn tangent to the starting and ending positions with dashed gray circles.
If the car has forward velocity of 1 unit per second, the system equations are
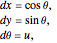
where 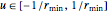 . The task is to minimize the length of the curve traced out by the center of the rear axle as it moves from the start to the goal. That path is the bounded-curvature shortest path. Dubins proved that the shortest path consists of no more than three segments, where in each segment
. The task is to minimize the length of the curve traced out by the center of the rear axle as it moves from the start to the goal. That path is the bounded-curvature shortest path. Dubins proved that the shortest path consists of no more than three segments, where in each segment  is either
is either 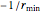 ,
,  or
or  . Denote these steering commands by R, S, L for turning right, going straight or turning left. A path is then coded with a three-letter word.
. Denote these steering commands by R, S, L for turning right, going straight or turning left. A path is then coded with a three-letter word.
If  , then the shortest path is a straight line. For nonzero
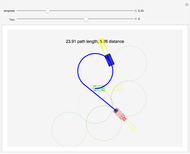
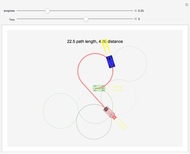
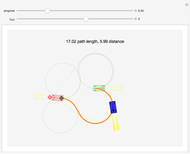
, then the shortest path is a straight line. For nonzero 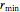 , the shortest paths are of the form LRL, RLR, LSL, LSR, RSL, RSR. In this Demonstration, each path type is given a different color: LRL is brown, RLR is dark green, LSL is pink, LSR is blue, RSL is orange, and RSR is dark yellow.
, the shortest paths are of the form LRL, RLR, LSL, LSR, RSL, RSR. In this Demonstration, each path type is given a different color: LRL is brown, RLR is dark green, LSL is pink, LSR is blue, RSL is orange, and RSR is dark yellow.
LSR (blue) and RSL (orange) are potentially valid only if the distance from start to goal is greater than 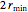 . The two paths composed entirely of curves, LRL (brown) and RLR (dark green), are potentially valid only if the distance from start to goal is less than
. The two paths composed entirely of curves, LRL (brown) and RLR (dark green), are potentially valid only if the distance from start to goal is less than 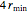 .
.
This Demonstration determines the shortest path by computing the paths using all of the valid words, and then picks the one with shortest length.
All paths are drawn in their respective colors, but the shortest path is drawn with a thicker line. Techniques in [4] show how to determine the regions where each path is optimal. If the car is allowed to move backward as well as forward, there are 46 possible words, and this mathematical model is called the Reeds–Shepp car [2].
References
[1] L. E. Dubins, "On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents," American Journal of Mathematics, 79(3), 1957 pp. 497–516. doi:10.2307/2372560.
[2] J. A. Reeds and L. A. Shepp, "Optimal Paths for a Car That Goes both Forwards and Backwards," Pacific Journal of Mathematics, 145(2), 1990 pp. 367–393. projecteuclid.org/euclid.pjm/1102645450.
[3] S. Lavalle, Planning Algorithms, Cambridge University Press, 2006. http://planning.cs.uiuc.edu/node821.html.
[4] X.-N. Bui, P. Souères, J.-D. Boissonnat and J.-P. Laumond, "The Shortest Path Synthesis for Non-holonomic Robots Moving Forwards," Research Report RR-2153, INRIA, France, 1994. hal.inria.fr/inria-00074519.
Permanent Citation