Side-Splitting Triangle Ratios

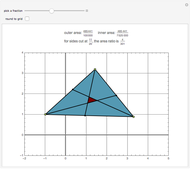
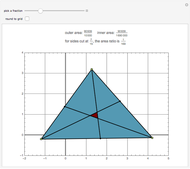
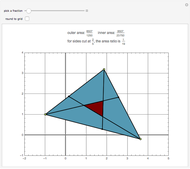
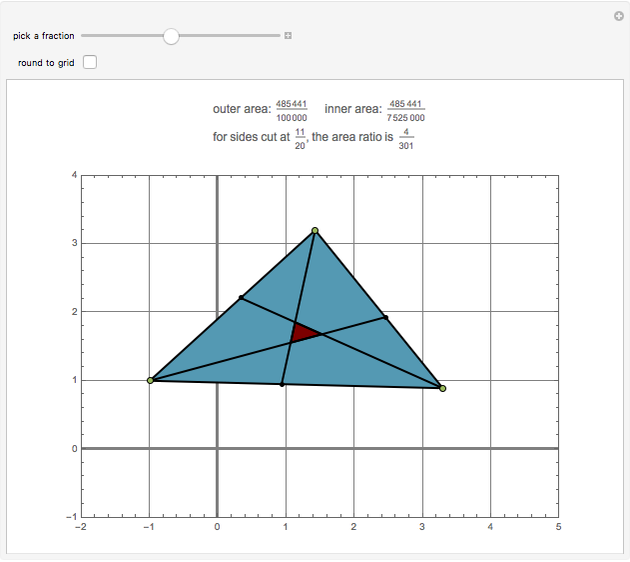
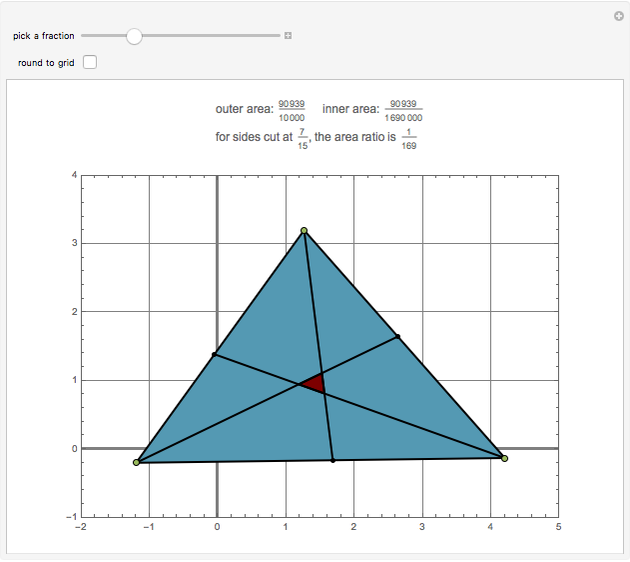
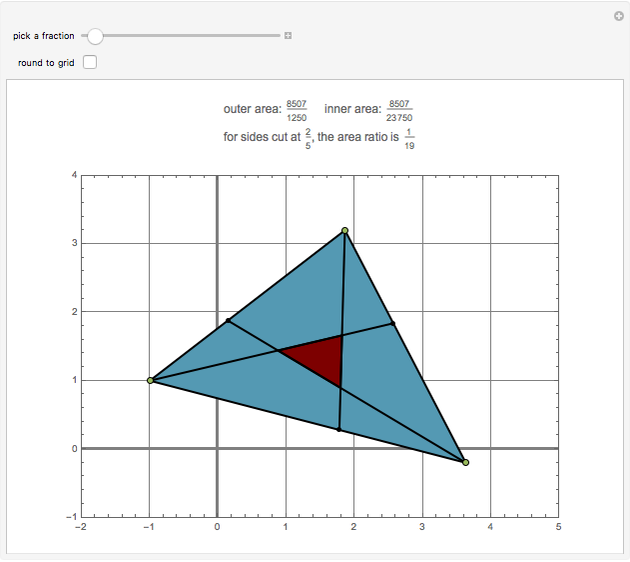
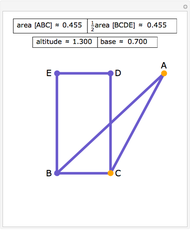
Going clockwise around a triangle, place a point on each side at position of the side's length. If segments are drawn from those points to the opposite vertex, the resulting inner triangle has area with ratio when compared to the area of the original triangle. For example, when each side is divided by thirds, the inner triangle is exactly one-seventh the area of the outer triangle.

This is a special case of Routh's theorem, which was proven by Edward Routh in 1896.