Simple Graphs and Their Binomial Edge Ideals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
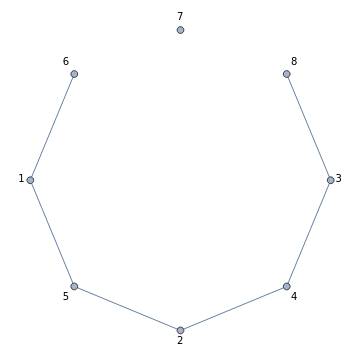
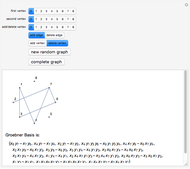
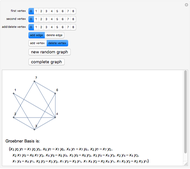
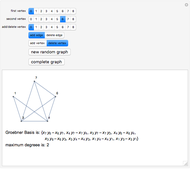
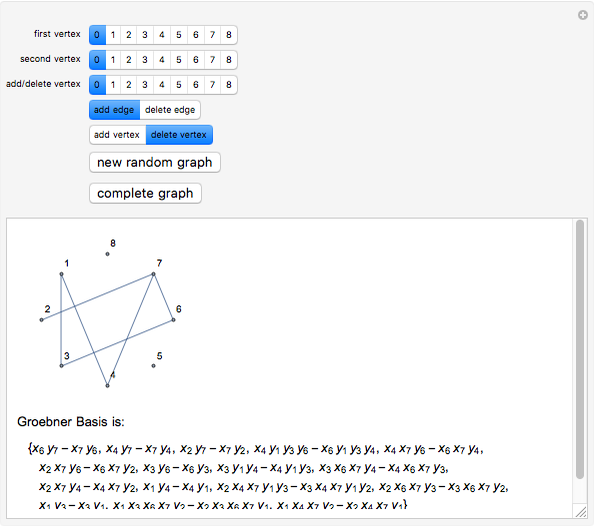
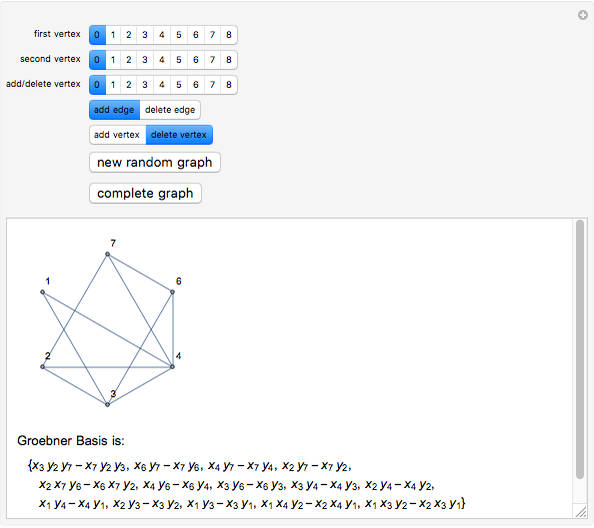
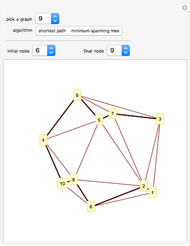
This Demonstration illustrates the relationship between combinatorial properties of a simple graph and its binomial edge ideal (see the Details section for definitions). In particular, it can be used to verify that a graph is closed (for a given ordering of vertices) if and only if the Groebner basis of its edge ideal consists of quadratic polynomials. By starting with a random graph that is not closed and adding suitable edges until the Groebner basis consists only of quadratic polynomials, you can find the closure of the graph, that is, the minimal closed graph containing the given graph. Alternatively, you can start with a complete graph (which is always closed) and remove edges (or vertices) to obtain non-closed graphs.
[more]
Contributed by: Andrzej Kozlowski (December 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let 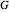 be a simple graph on the vertex set
be a simple graph on the vertex set 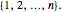 We say that the graph is closed with respect to the given ordering of vertices if
We say that the graph is closed with respect to the given ordering of vertices if 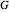 satisfies the condition that for any pair of edges
satisfies the condition that for any pair of edges  and
and 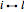 with
with 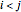 and
and 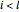 , the edge
, the edge 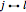 is an edge of
is an edge of 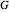 and for any pair of edges
and for any pair of edges  and
and 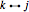 with
with 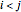 and
and  the edge
the edge  is an edge of
is an edge of 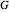 .
.
For a field 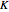 , let
, let 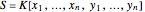 be the ring of polynomials in
be the ring of polynomials in  variables. The binomial edge ideal
variables. The binomial edge ideal  is the ideal generated by the elements
is the ideal generated by the elements 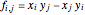 where
where 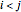 and
and  is an edge of
is an edge of 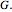 Binomial edge ideals of graphs were introduced in [1] and play a role in the study of conditional independence statements and the subject of algebraic statistics [2]. In this Demonstration we illustrate theorem 1.1 of (1), which states that a simple graph
Binomial edge ideals of graphs were introduced in [1] and play a role in the study of conditional independence statements and the subject of algebraic statistics [2]. In this Demonstration we illustrate theorem 1.1 of (1), which states that a simple graph 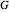 is closed (for a given ordering) if and only if the reduced Gröbner basis of its binomial edge ideal
is closed (for a given ordering) if and only if the reduced Gröbner basis of its binomial edge ideal 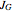 with respect to the lexicographic ordering on
with respect to the lexicographic ordering on 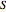 induced by
induced by 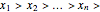
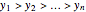 is quadratic (and generated by
is quadratic (and generated by  ).
).
References
[1] J. Herzog, T. Hibi, F. Hreinsdóttir, F. Kahle, and T. Rauh, "Binomial Edge Ideals and Conditional Independence Statements," arXiv:0909.4717, 2009.
[2] M. Drton, B. Sturmfels, and S. Sullivant, Lectures on Algebraic Statistics, Vol. 39, Berlin: Springer, 2009.
Permanent Citation