Simulating a Minimal ORAC Kinetic System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Contributed by: Juan B. Arellano, Elena Mellado-Ortega and K. Razi Naqvi (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
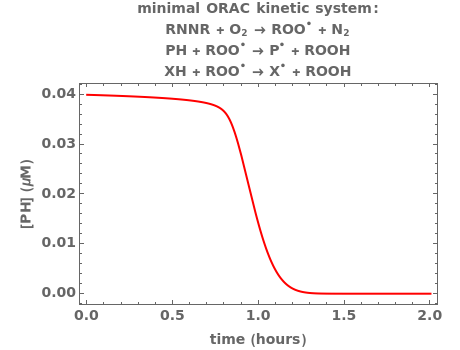
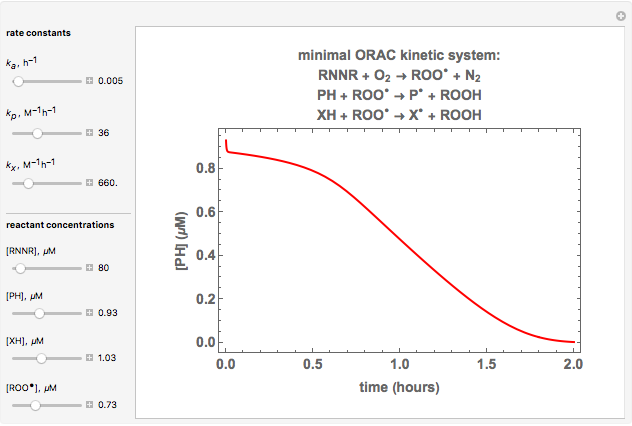
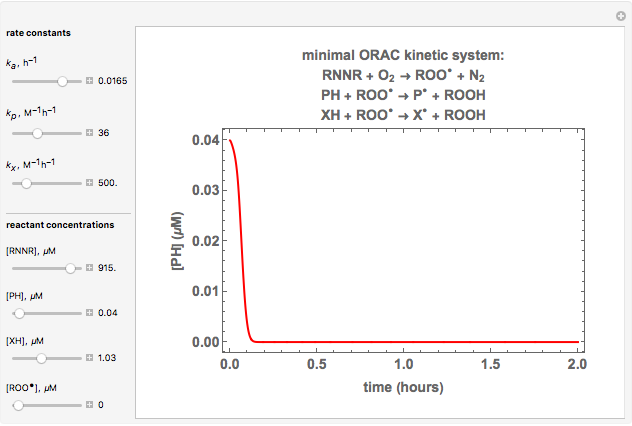
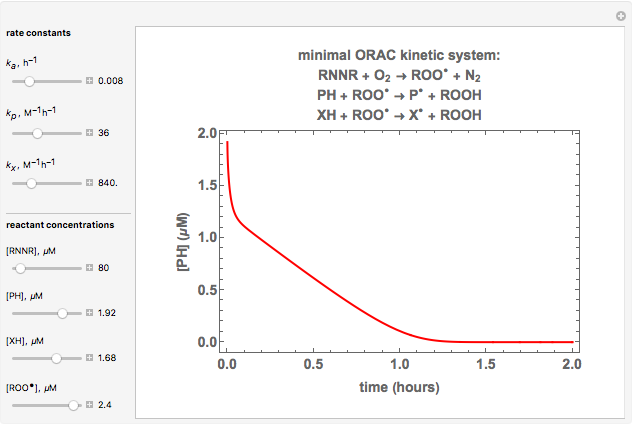
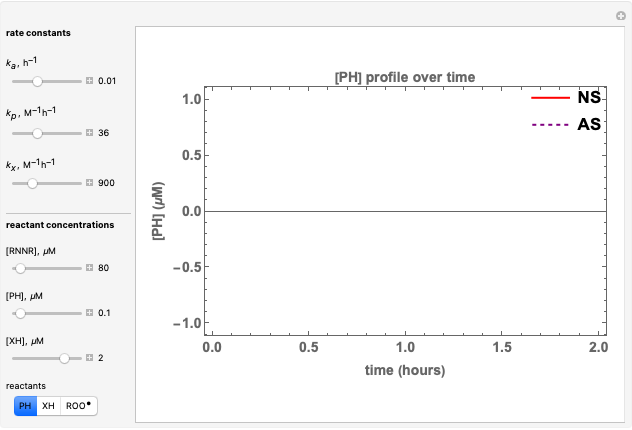
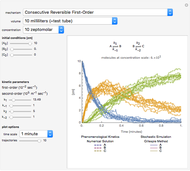
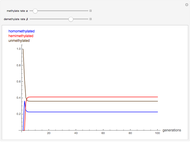
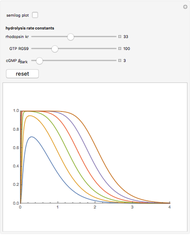
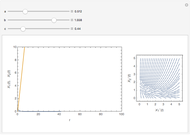
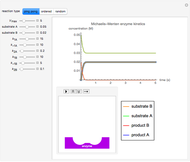
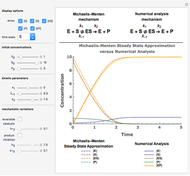
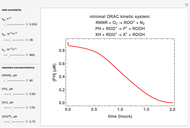
Oxygen radical absorbance capacity (ORAC) assay is widely used for determining the total antioxidant activity of samples in vitro. In brief, ORAC is based on a hydrogen atom transfer reaction in which the solvent-extracted antioxidants of a sample compete with a probe for tertiary peroxyl radicals, which in turn are formed in the reaction mixture by thermolysis of an azo compound whose carbon-centered radical rapidly reacts with dissolved oxygen. The overall minimal ORAC kinetic system can be represented by three reactions: one apparent first-order step and two second-order reactions following a consecutive-parallel cascade with three starting reactants:
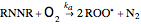 (R.1)
(R.1)
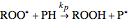 (R.2)
(R.2)
 (R.3),
(R.3),
where 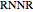 ,
, 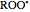 ,
, 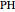 and
and 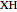 stand for the azo compound, the tertiary azo compound-derived peroxyl radical, the probe and the antioxidant, respectively, while
stand for the azo compound, the tertiary azo compound-derived peroxyl radical, the probe and the antioxidant, respectively, while 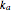 ,
, 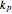 and
and 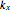 represent the apparent first- and second-order rate constants of the (R.1)–(R.3) reactions, respectively.
represent the apparent first- and second-order rate constants of the (R.1)–(R.3) reactions, respectively.
In a more complex ORAC kinetic system, peroxyl and alkoxyl radical self-reactions are included in the kinetic system, in addition to the reactions (R.1)–(R.3). However, the former reactions add complexity to the mathematical analysis and experimental conditions can be chosen to justify the neglect of the peroxyl and alkoxyl radical self-reactions. For example, when the initial concentration of the azo-compound radical initiator is low, we opted to exclude the peroxyl and alkoxyl self-reactions from our mathematical analysis [1].
Reference
[1] J. B. Arellano, E. Mellado-Ortega and K. R. Naqvi, "The ORAC Assay: Mathematical Analysis of the Rate Equations and Some Practical Considerations," International Journal of Chemical Kinetics, 2017, doi:10.1002/kin.21086.
Permanent Citation