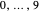Simulating the Coupon Collector Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
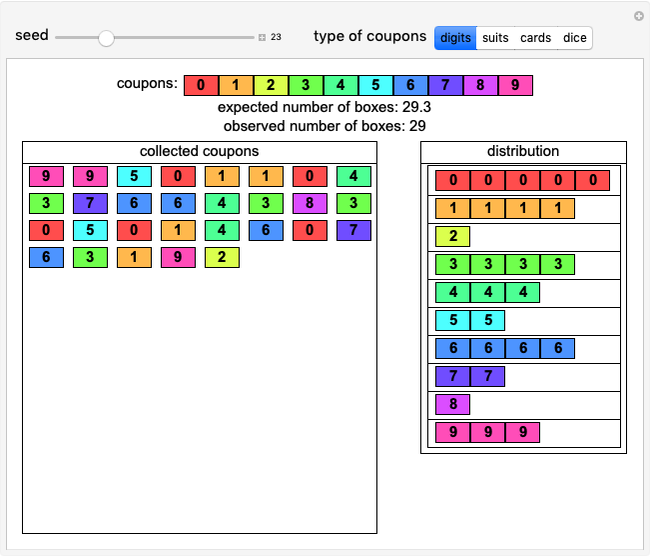
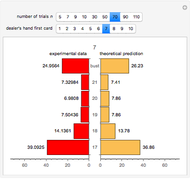
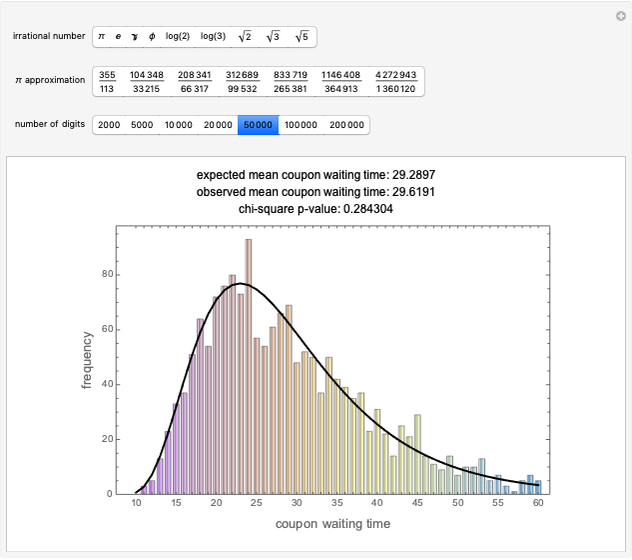
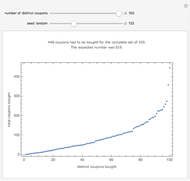
A statement of the coupon collector problem: suppose each box of cereal contains a coupon chosen at random from 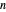 possible coupons. Let
possible coupons. Let 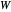 be the number of boxes of cereal that need to be purchased in order to get a complete set of all
be the number of boxes of cereal that need to be purchased in order to get a complete set of all 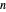 coupons. What is the expected value (or waiting time) of
coupons. What is the expected value (or waiting time) of 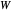 ? The answer is given by the formula
? The answer is given by the formula 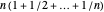 .
.
Contributed by: Yikai Teng (May 2019)
Based on an undergraduate research project at the Illinois Geometry Lab by Raymond Harpster, Tianli Li, Yikai Teng and directed by A. J. Hildebrand.
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] B. Dawkins, "Siobhan's Problem: The Coupon Collector Revisited," The American Statistician, 45(1), 1991 pp. 76–82. doi:10.1080/00031305.1991.10475772.
Permanent Citation