Simulating the Poisson Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
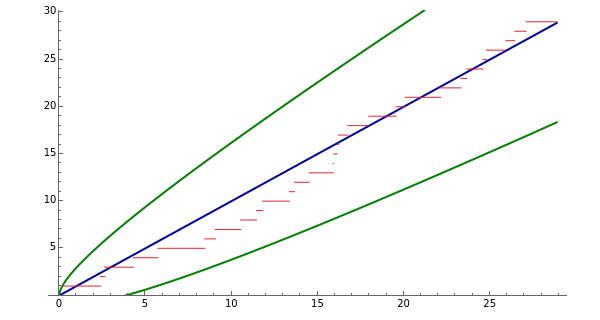
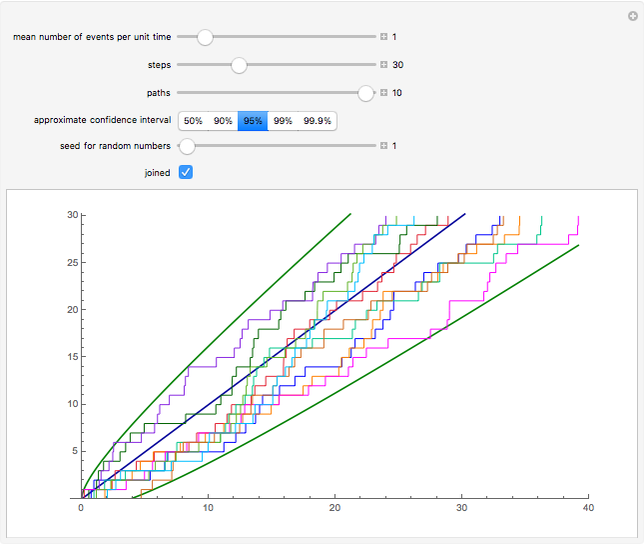
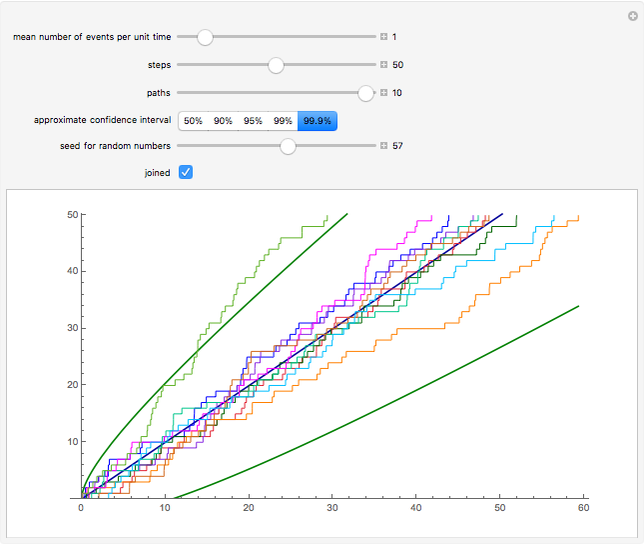
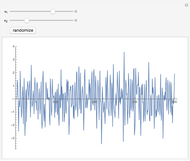
This Demonstration shows simulated paths of the Poisson process. You can see how the cumulative number of events increases as time lapses. You can adjust the mean number of events per unit time. The Demonstration also shows the mean of the process (the blue line) and approximate confidence intervals (the green curves). The confidence intervals are based on the normal approximation to the Poisson distribution. The Poisson process is a special case of a continuous-time Markov chain.
Contributed by: Heikki Ruskeepää (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
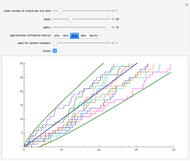
Snapshot 1: unjoined paths
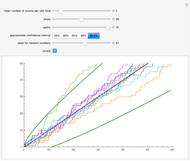
Snapshot 2: joined paths
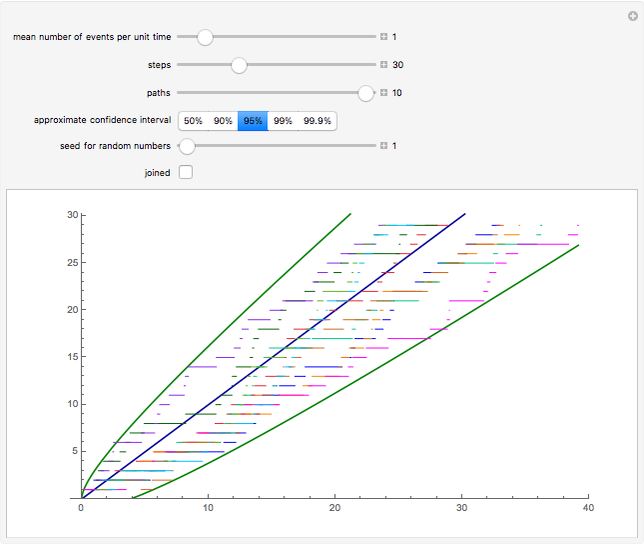
Snapshot 3: one of the paths goes outside of the 99.9% confidence interval
Snapshots 1 and 2 are the same except that in Snapshot 2 the paths are joined. These snapshots show that when you show several paths, joining the paths with vertical lines makes the paths clearer.
Recall that in a Poisson process events occur randomly in time. If time starts at 0, then the number of events occurring up to time  is a random variable that has a Poisson distribution with mean
is a random variable that has a Poisson distribution with mean  . Here,
. Here, 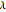 is the mean number of events that occur in one unit of time. The time between the events has an exponential distribution with mean
is the mean number of events that occur in one unit of time. The time between the events has an exponential distribution with mean 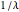 .
.
For the Poisson process, see [1, pp. 204–208]. For simulation of the Poisson process and other stochastic processes with Mathematica, see [2, pp. 987–1002]. Andrzej Kozlowski has also created a Demonstration, The Poisson Process, that shows simulated paths of the Poisson process. That Demonstration also shows so-called compensated Poisson processes but does not show the mean or confidence intervals.
[1] A. O. Allen, Probability, Statistics, and Queueing Theory with Computer Science Applications, 2nd ed., Boston: Academic Press, 1990.
[2] H. Ruskeepää, Mathematica Navigator: Mathematics, Statistics, and Graphics, 3rd ed., San Diego, CA: Elsevier Academic Press, 2009.
Permanent Citation
"Simulating the Poisson Process"
http://demonstrations.wolfram.com/SimulatingThePoissonProcess/
Wolfram Demonstrations Project
Published: March 7 2011