Simulating the Simple Random Walk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
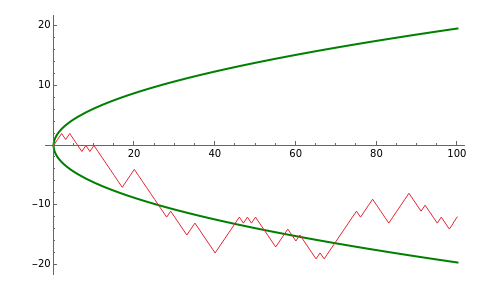
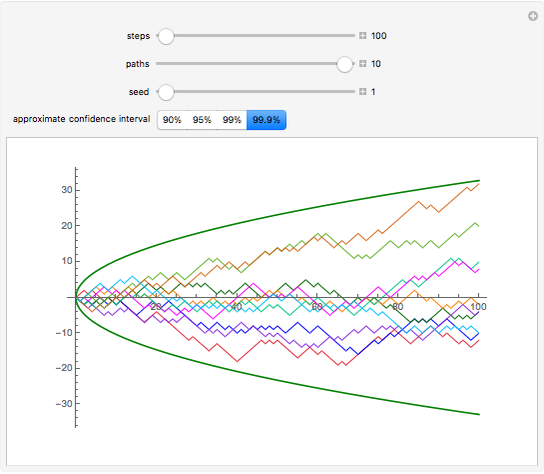
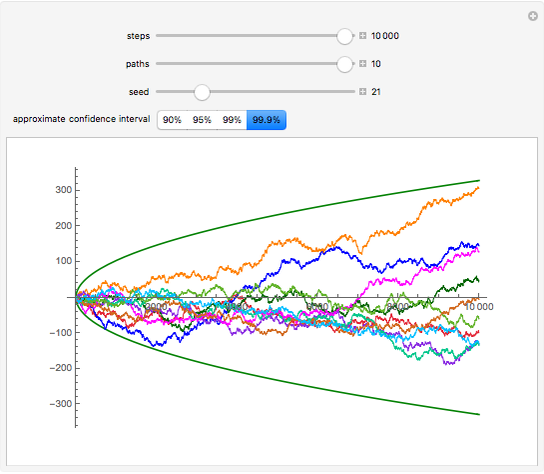
This Demonstration shows simulated paths of the simple random walk. Thus, you can see how the path evolves with time. The Demonstration also shows approximate confidence intervals (the green curves), which are based on the normal approximation.
Contributed by: Heikki Ruskeepää (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
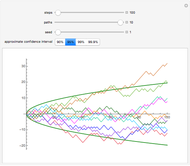
Snapshot 1: some of the 10 paths go outside of the 95% confidence interval
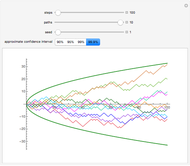
Snapshot 2: all 10 paths stay within the 99.9% confidence interval
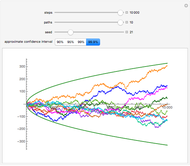
Snapshot 3: 10 paths, each of 10,000 steps, 99.9% confidence interval
The simple random walk starts at 0. At each time step  , 1 is added or subtracted from the current value. Addition and subtraction are done with equal probabilities. In the plots, the values
, 1 is added or subtracted from the current value. Addition and subtraction are done with equal probabilities. In the plots, the values 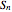 are plotted on the vertical axis and the time axis is horizontal.
are plotted on the vertical axis and the time axis is horizontal.
The confidence intervals can be obtained from the following result. Let 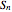 be the position of the walk at step
be the position of the walk at step  . The probability that
. The probability that 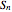 is greater than
is greater than 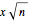 approaches, as
approaches, as  approaches infinity, the probability that the standard normal variable is greater than
approaches infinity, the probability that the standard normal variable is greater than  ; see [1], p. 76.
; see [1], p. 76.
For the simple random walk, see [1], pp. 67–97. For simulation of the simple random walk and other stochastic processes with Mathematica, see [2], pp. 987–1002.
[1] W. Feller, An Introduction to Probability and Its Applications, vol. 1, 3rd ed., revised printing, New York: Wiley, 1968.
[2] H. Ruskeepää, Mathematica Navigator: Mathematics, Statistics, and Graphics, 3rd ed., San Diego, CA: Elsevier Academic Press, 2009.
Permanent Citation