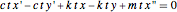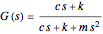Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Simulating Vehicle Suspension with a Simplified Quarter-Car Model

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

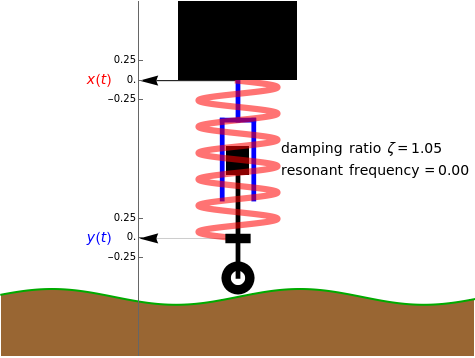
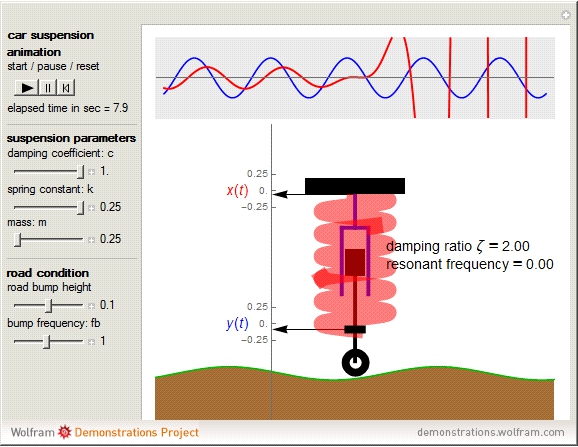
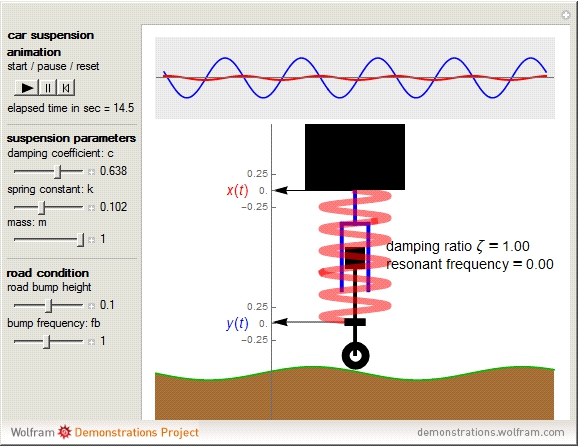
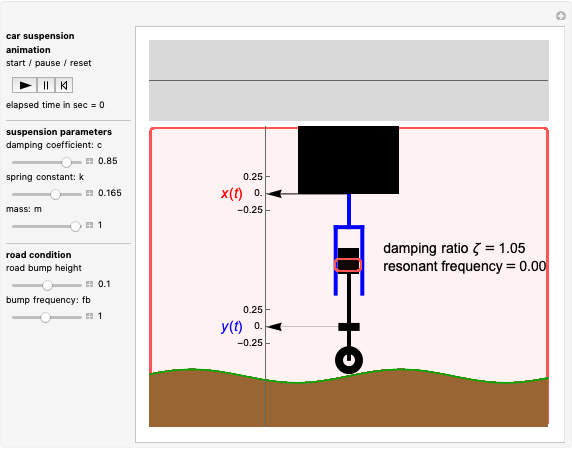
The simplified quarter-car suspension model is basically a mass-spring-damper system with the car serving as the mass, the suspension coil as the spring, and the shock absorber as the damper.

[more]

This Demonstration lets you explore the affect of different suspension parameters and road conditions on the vertical motion of the car.

The mathematics of the system are based on the differential equation of the spring-damper suspension: , which, after a Laplace transform, results in the transfer function .
The Mathematica 8 functions TransferFunctionModel and OutputResponse were used to calculate the car movement with no need to solve the differential equation.

[less]

Contributed by: Erik Mahieu (January 2019)
Open content licensed under CC BY-NC-SA

Details

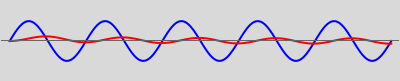
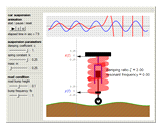
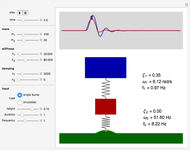
Snapshot 1: very hard suspension with a light car gives excessive shaking

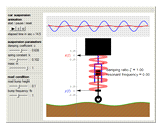
Snapshot 2: the damping ratio is 1 and gives optimal comfort

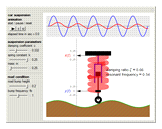
Snapshot 3: at resonant frequency, a maximum car movement is obtained

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send