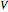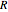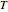Simulation of a Simple Gas Pressure Model

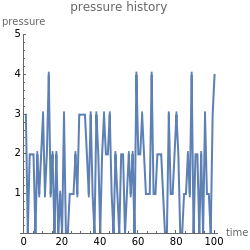
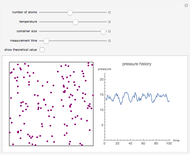
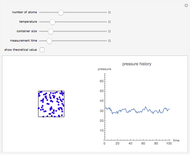
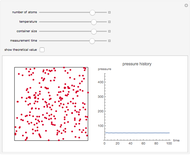
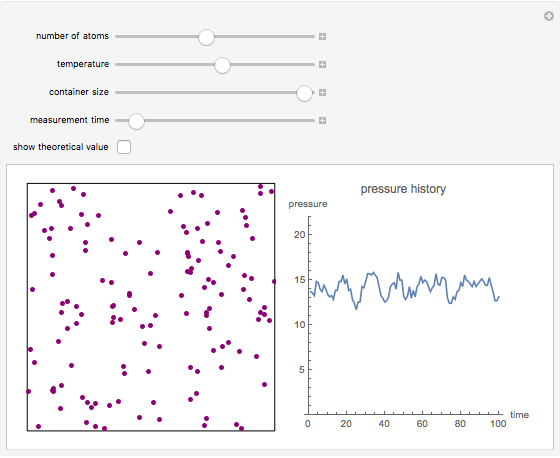
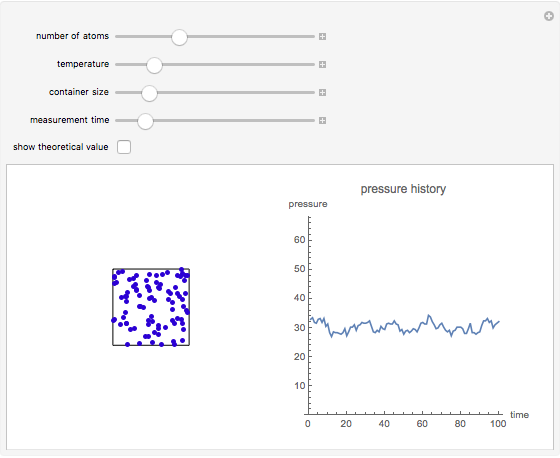
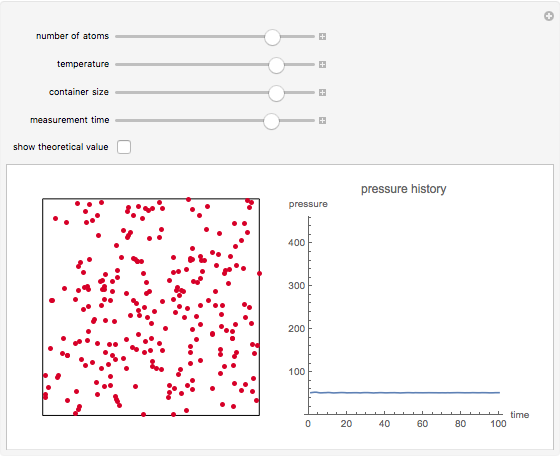
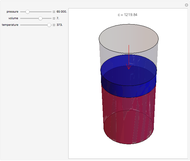
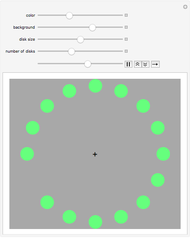
This simple model to understand gas pressure considers the gas as a collection of independent molecules bouncing inside a container and counts the frequency of collisions on the container's walls. Pressure, then, equals the force per unit area . Larger numbers of discrete impulses of force can be averaged over an observation time to give an apparently constant pressure.

Release particles of gas by increasing the "number of atoms" slider or by clicking in the box, then watch the pressure graph register the impacts. Increasing the "measurement time" allows for smoother counts at the expense of less responsive measurement.

As predicted by the ideal gas law and Boyle's Law, the pressure can be increased by reducing the size of the container or by increasing the number of molecules or the temperature (speed of the atoms).

The ideal gas law states that:

,

where is the pressure, is the volume, is the amount of gas, is the gas constant, and is the temperature of the gas.

Pressure can be defined as , where is the force applied by the gas and is the surface area.

In this two-dimensional analogy, pressure is taken to be , where is the length.