Simultaneous Approximation of Two Real Numbers by Rationals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
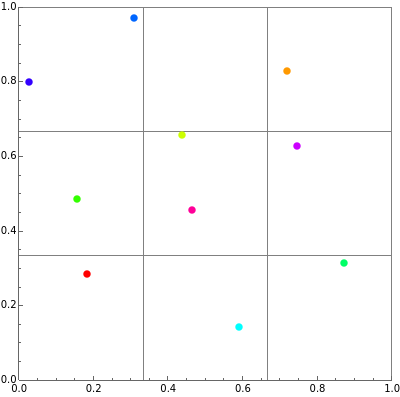
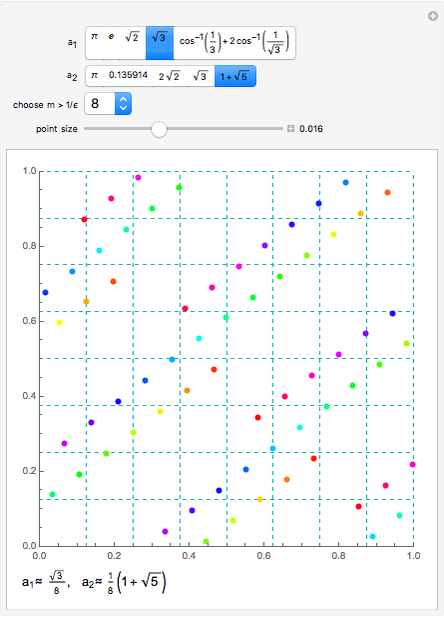
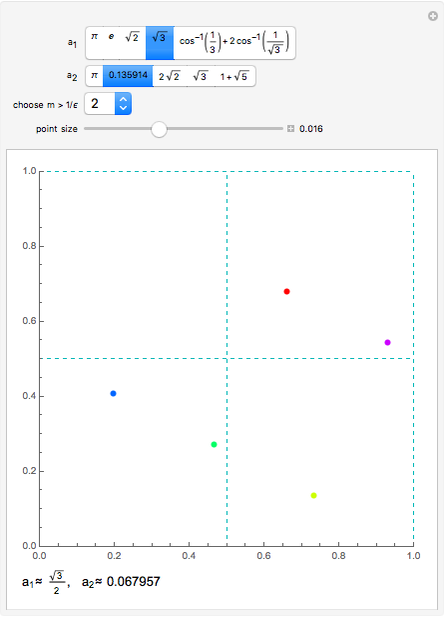
This Demonstration illustrates the simultaneous approximation of two real numbers by rational numbers, because there is always a small square with at least two points.
Contributed by: Mateja Budin (March 2011)
Proposed by: Izidor Hafner
Open content licensed under CC BY-NC-SA
Snapshots
Details
Lemma 1. Let 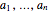 be real numbers. For each
be real numbers. For each  it is possible to approximate
it is possible to approximate 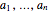 simultaneously by rational numbers
simultaneously by rational numbers 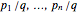 , in the sense that
, in the sense that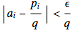 (
( ). In addition, if all
). In addition, if all 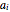 are positive, then the
are positive, then the 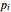 can be chosen to be positive, where
can be chosen to be positive, where  is replaced with
is replaced with 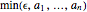 .
.
Proof. Let 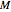 be a positive integer satisfying
be a positive integer satisfying 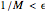 . Then by the pigeonhole principle, among the
. Then by the pigeonhole principle, among the 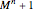 points
points 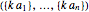 (
( ), where
), where 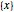 denotes the fractional part of
denotes the fractional part of  , there are at least two numbers
, there are at least two numbers  such that
such that 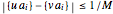 for all
for all  . Then
. Then 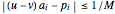 for some integers
for some integers 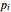 . The statement is proved if we put
. The statement is proved if we put 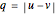 .
.
This lemma was used in the elementary proof of Hilbert's third problem.
Reference
[1] D. Benko, "A New Approach to Hilbert's Third Problem," American Mathematical Monthly 114(8), 2007 pp. 665–676.
Permanent Citation