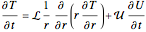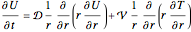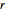Simultaneous Heat and Moisture Transfer in a Porous Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
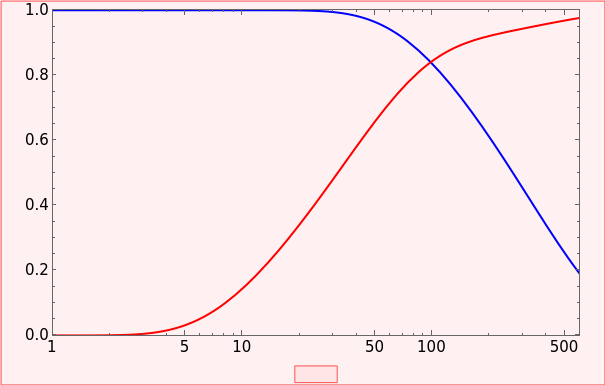
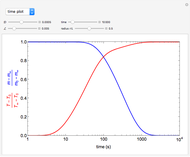
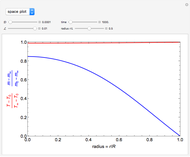
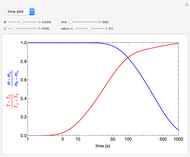
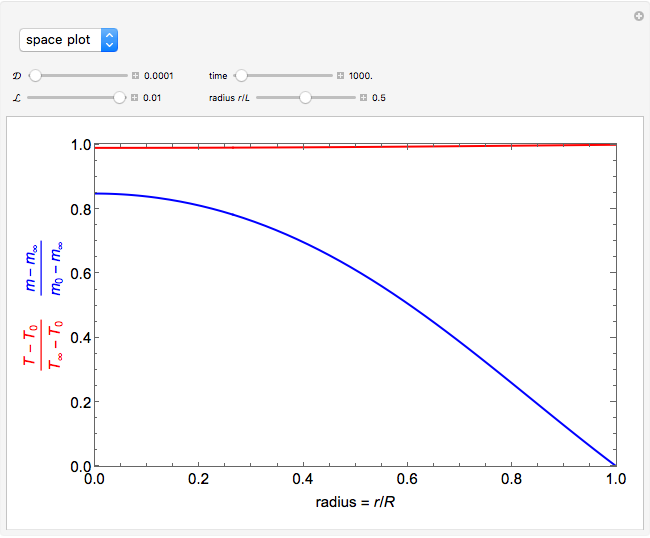
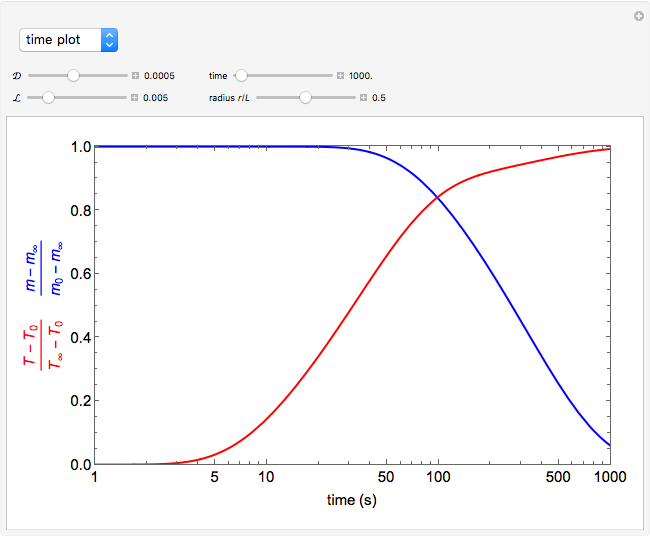
This Demonstration illustrates a model of heat and moisture transfer accompanied by phase change in a porous cylinder. The porous cylinder is initially at a constant temperature and moisture. It is suddenly placed in contact with a stream of hot air that exchanges heat and moisture by diffusion and convection. The moisture movement and the phase change occurring within the cylinder generate a coupled relationship between mass and heat transfer.
[more]
Contributed by: Clay Gruesbeck (January 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Luikov equation coefficients are:

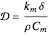
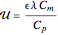
 .
.
The moisture potential is related to moisture content by  . The cylinder is assumed to have an infinite length to radius ratio, thus only radial transport is considered; material properties are assumed to be constant.
. The cylinder is assumed to have an infinite length to radius ratio, thus only radial transport is considered; material properties are assumed to be constant.
Nomenclature
 moisture capacity
moisture capacity 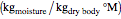
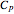 heat capacity
heat capacity 
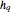 convective heat transfer coefficient
convective heat transfer coefficient 
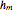 convective mass transfer coefficient
convective mass transfer coefficient 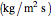
 moisture conductivity
moisture conductivity 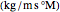
 thermal conductivity
thermal conductivity 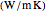
 moisture
moisture 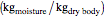
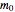 initial cylinder moisture
initial cylinder moisture 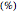
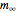 moisture of the air
moisture of the air 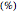
 cylinder radius
cylinder radius 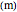
 space coordinate
space coordinate 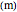
 time
time 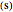
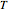 temperature
temperature 
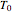 initial cylinder temperature
initial cylinder temperature 
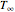 temperature of the air
temperature of the air 

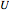 moisture potential
moisture potential 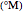
Symbols
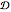 equivalent moisture diffusion coefficient
equivalent moisture diffusion coefficient 
 thermo-gradient coefficient
thermo-gradient coefficient 
 ratio of vapor diffusion coefficient to coefficient of total diffusion of moisture
ratio of vapor diffusion coefficient to coefficient of total diffusion of moisture
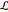 equivalent temperature diffusion coefficient
equivalent temperature diffusion coefficient 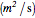
 heat of vaporization
heat of vaporization 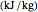
 density
density 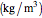
 coupling coefficient due to moisture migration
coupling coefficient due to moisture migration 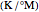
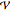 coupling coefficient due to heat conduction
coupling coefficient due to heat conduction 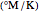
At the boundary of the cylinder, the latent heat of vaporization becomes part of the energy balance, and the mass diffusion caused by the temperature and moisture gradients affects the overall mass balance; the boundary conditions at 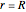 are:
are:
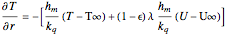
and
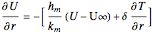 .
.
The right-hand side of the first boundary condition represents the heat flux due to convection plus the energy transfer due to phase change, and the right-hand side of the second condition represents the mass flux due to convection plus the mass flux due to the temperature gradient.
At 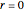 because of symmetry we have:
because of symmetry we have:
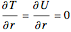 .
.
The initial conditions are
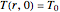
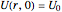 .
.
The system of Luikov equations is solved using the finite element method as implemented in the built-in Mathematica function NDSolve, and the results are presented in space and time plots for various values of the temperature and moisture diffusion coefficients  and
and  .
.
Reference
[1] H. R. Thomas, R. W. Lewis and K. Morgan, "An Application of the Finite Element Method to the Drying of Timber," Wood and Fiber Science: Journal of the Society of Wood Science and Technology, 11(4), 1980 pp. 237–243. wfs.swst.org/index.php/wfs/article/download/534/534.
Permanent Citation