Sine Oval and Nested Trig Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
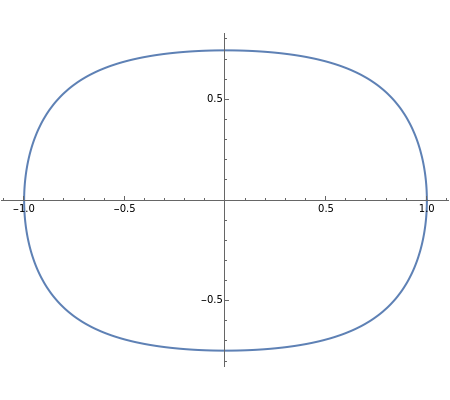
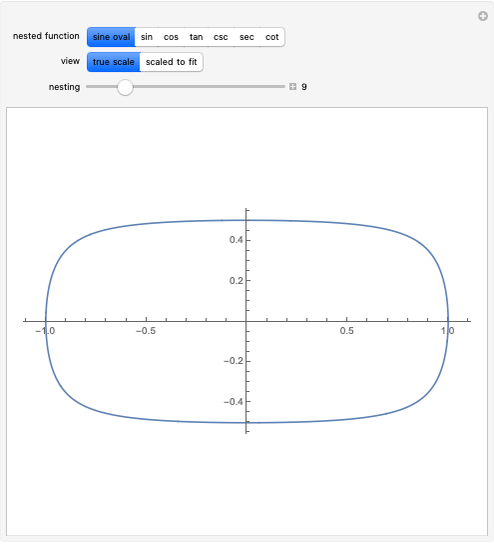
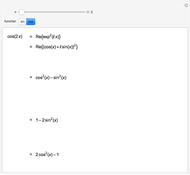
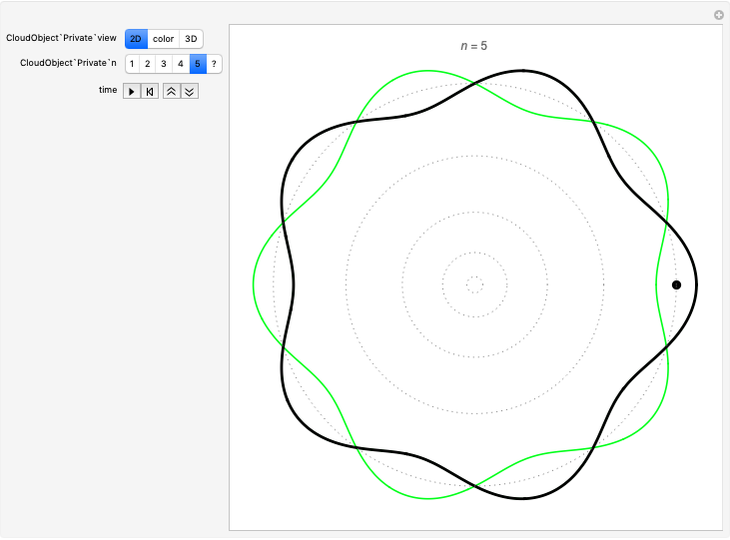
The unit circle is the set of all points  , but nesting the sine function in this formula,
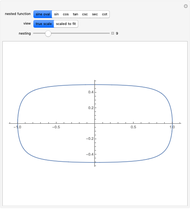
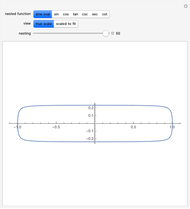
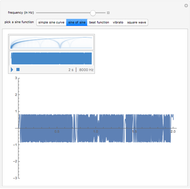
, but nesting the sine function in this formula, 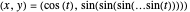 , gives the sine oval, which becomes progressively more squarish with increased levels of nesting (controlled by the slider). Change the graph to "sin" to examine the nested sine function alone, whose squarish behavior is not shared by the other trig functions.
, gives the sine oval, which becomes progressively more squarish with increased levels of nesting (controlled by the slider). Change the graph to "sin" to examine the nested sine function alone, whose squarish behavior is not shared by the other trig functions.
Contributed by: Kenneth E. Caviness (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
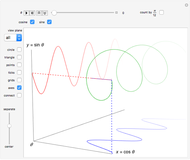
The sine oval [1] is plotted using the command
ParametricPlot[{Cos[t], Nest[Sin, t, n]}, {t, 0, 2 Pi}],
where  is some positive integer. Using
is some positive integer. Using 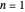 gives the unit circle. If
gives the unit circle. If 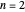 , the
, the 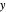 coordinate is given by
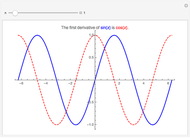
coordinate is given by 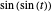 , and increasing the nesting of the sine function results in an increasingly squarish oval. Similarly, a plot of the nested sine function approaches a simple square wave of decreasing amplitude [2].
, and increasing the nesting of the sine function results in an increasingly squarish oval. Similarly, a plot of the nested sine function approaches a simple square wave of decreasing amplitude [2].
It is logical to also inquire what happens if other trigonometric functions are nested, but it turns out that their behavior is quite different: the nested cosine function never becomes square but approaches and oscillates about a constant value of 0.739085…. The other basic trig functions show increasing regions of oscillation, generally between +∞ and -∞. The exception is cosecant, which in an increasing number of intervals of decreasing size approaches +1 or -1, and is undefined at the boundaries of these intervals.
References:
[1] W. Gu, The Sine Oval; The Library of Curves.
[2] T. Gray and J. Glynn, Exploring Mathematics with Mathematica, Reading, MA: Addison–Wesley, 1991.
Permanent Citation