Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

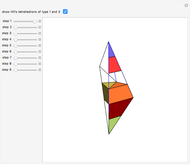
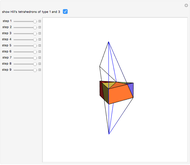
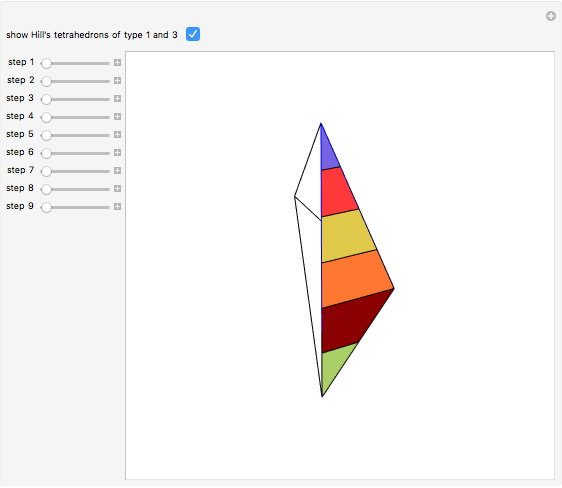
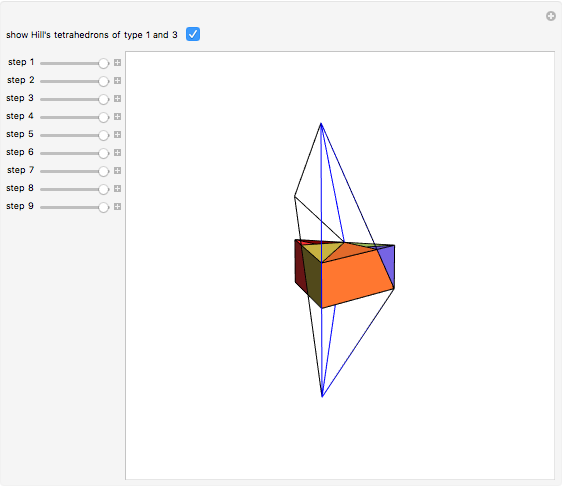
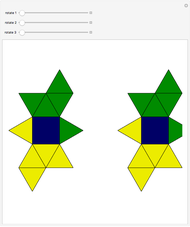
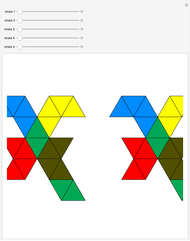
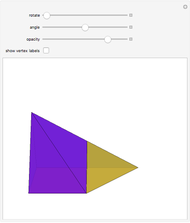
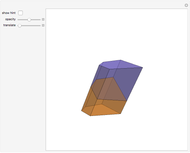
Six-Piece Dissection of Hill's Tetrahedron of Type 3 into a Triangular Prism

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

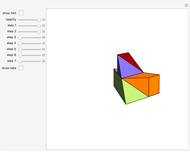
This Demonstration gives a six-piece dissection of Hill's tetrahedron of type 3 into a triangular prism.

Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The dissection was discovered by P. Schöbi (1985). G. N. Frederickson, Dissections: Plane & Fancy, New York: Cambridge University Press, 2002 pp. 235–236.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send