Slope between Two Points on a Curve
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
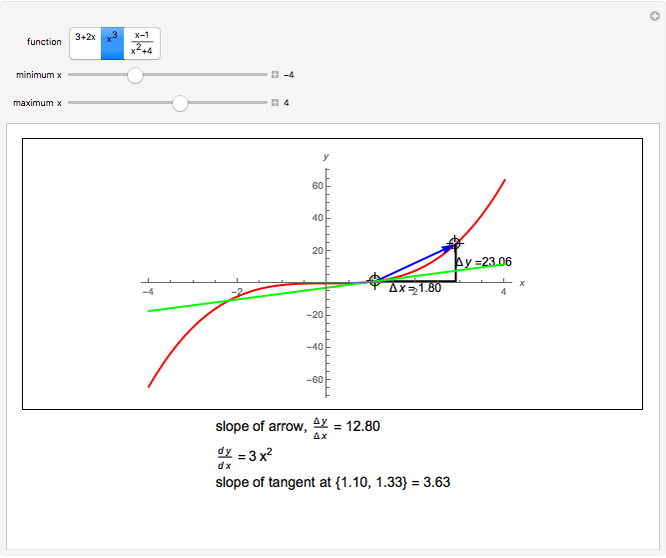
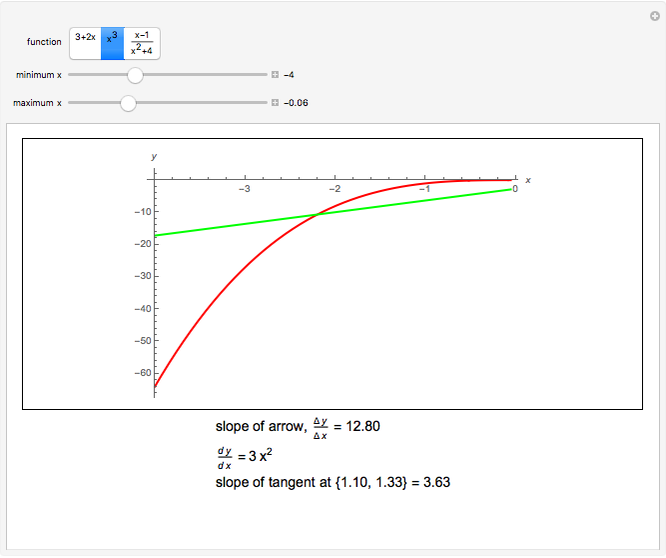
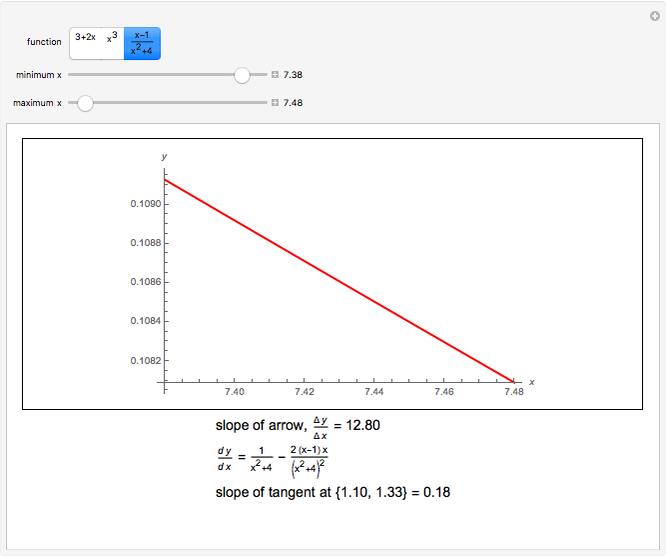
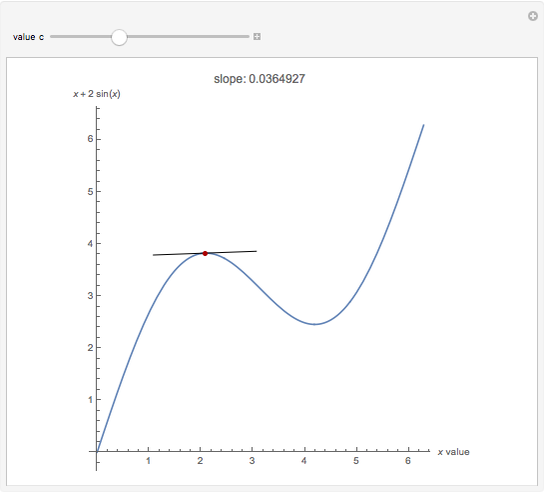
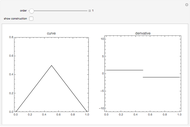
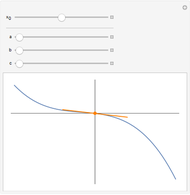
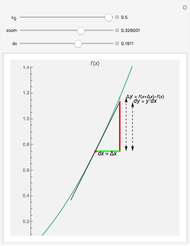
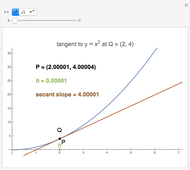
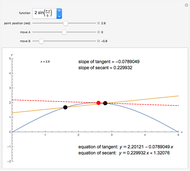
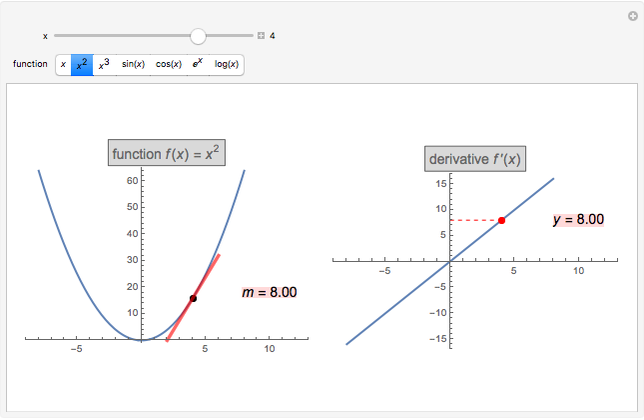
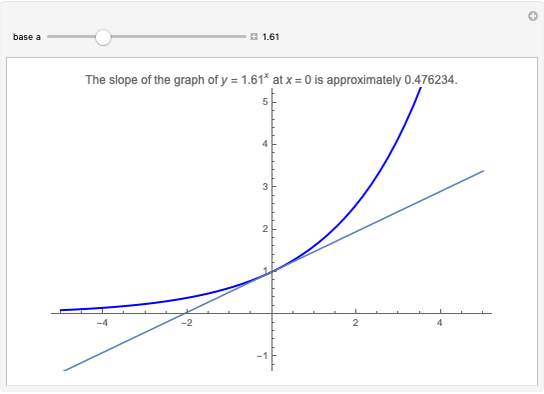
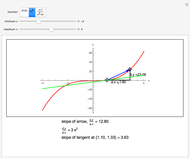
Calculate the slope between two points on one of three curves by dragging the locators. As the locators get close enough, the slope gets closer to the slope of the tangent line, which is the value of the derivative of the function at the point.
Contributed by: Trevor Cole (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The slope between two points, joined in the diagram by an arrow is calculated. The tangent at the point at the base of the arrow is calculated from the derivative of the function. The tangent line is shown in green.
It can be seen with a suitable choice of parameters that:
a straight line has a constant slope, and
the slope between two points approaches the tangent, as the distance between the points decreases.
Permanent Citation
"Slope between Two Points on a Curve"
http://demonstrations.wolfram.com/SlopeBetweenTwoPointsOnACurve/
Wolfram Demonstrations Project
Published: March 7 2011
Fermat's Theorem on Stationary Points
Julio Cesar de la Yncera
Family of Curves, Tangents, and Intuition
Jacqueline Zizi
Takagi Curve
Borut Levart
Tangent to a Curve
Stephen Wolfram
Geometric Difference between a Finite Difference and a Differential
Anping Zeng (Sichuan Chemical Technical College)
The Tangent Line Problem
Samuel Leung and Michael Largey
Approximating the Tangent to a Curve with Secants
Stephen Wilkerson (Towson University)
Derivatives of the Sum of Two Sines
Denis Shubleka
Derivative as a Function
Jim Brandt
The Derivative of a to the Power x
Jerry Stanbrough
