Small Intervals where the Partial Sums of a Series Fail to Alternate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
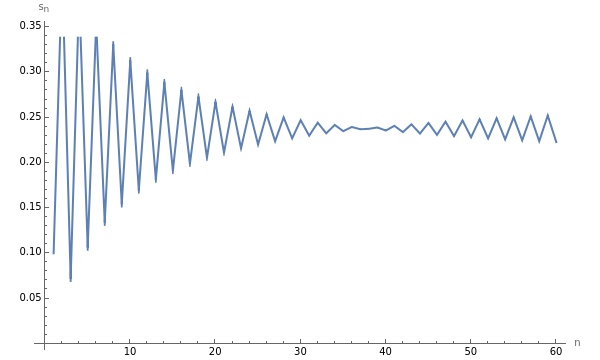
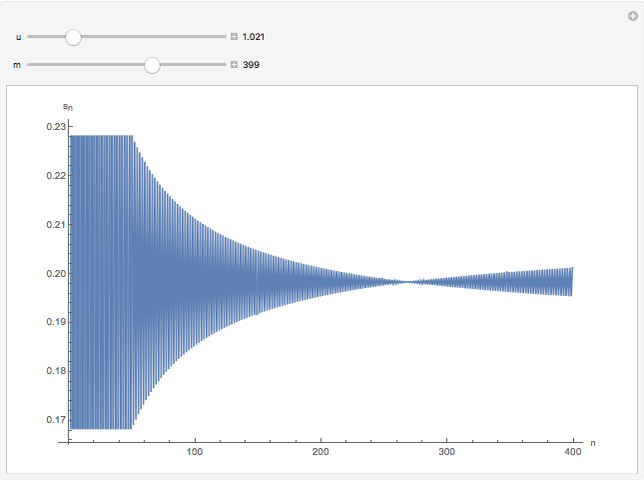
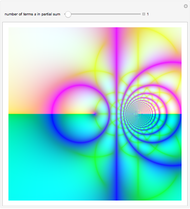
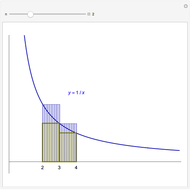
Consider the variant 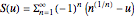 of the series
of the series 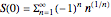 , where
, where  is a non-negative parameter. For
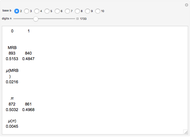
is a non-negative parameter. For  , the partial sums
, the partial sums 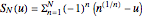 of
of  alternate as
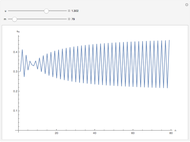
alternate as  gets large. However, for values of
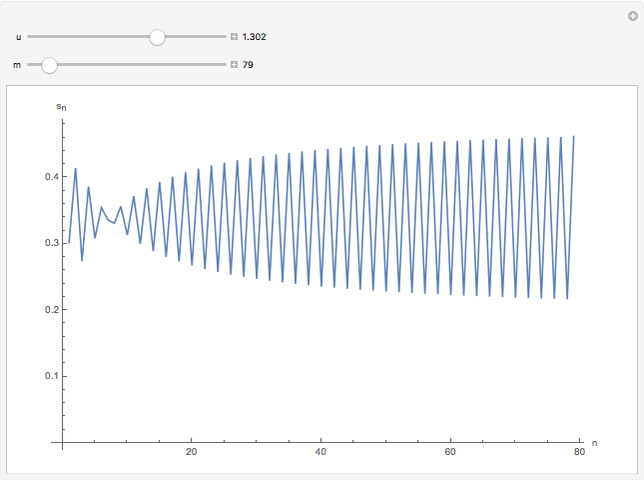
gets large. However, for values of  in a certain range, there will be a small interval where the sequence of partial sums fails to alternate. That is, there is an
in a certain range, there will be a small interval where the sequence of partial sums fails to alternate. That is, there is an 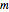 such that
such that 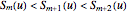 or the reverse,
or the reverse,  . It might be an interesting exercise to understand this visually paradoxical phenomenon (see Details for an outline).
. It might be an interesting exercise to understand this visually paradoxical phenomenon (see Details for an outline).
Contributed by: Marvin Ray Burns (March 2011)
With additional contributions by the Wolfram Demonstrations team.
Open content licensed under CC BY-NC-SA
Snapshots
Details
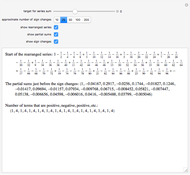
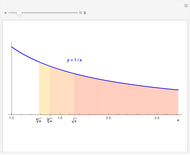
For 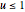 , there are no skips in the alternations of the partial sums. In order to have such a skip, there must be a sign change between
, there are no skips in the alternations of the partial sums. In order to have such a skip, there must be a sign change between  and
and  . This is equivalent to having exactly one root of
. This is equivalent to having exactly one root of 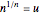 in
in  . It can be shown that this happens for
. It can be shown that this happens for 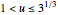 . For
. For  we still have two real roots to this equation, but both are in the interval
we still have two real roots to this equation, but both are in the interval  . Hence there is no sign change (because there were two skips within the same unit interval). For
. Hence there is no sign change (because there were two skips within the same unit interval). For  , there are no longer real solutions to the equation
, there are no longer real solutions to the equation 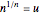 . Also notice that for
. Also notice that for  , we have a root for
, we have a root for  and another with
and another with  . Hence we have consecutive sign changes. For
. Hence we have consecutive sign changes. For  in this range, we have an initial sequence of three partial sums decreasing after the first term.
in this range, we have an initial sequence of three partial sums decreasing after the first term.
Permanent Citation