Some Gaussian Integrals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The well-known Gaussian integral  can be evaluated in closed form, even though there is no elementary function equal to the indefinite integral
can be evaluated in closed form, even though there is no elementary function equal to the indefinite integral  . More generally, integrals of the form
. More generally, integrals of the form  can be evaluated for positive integers
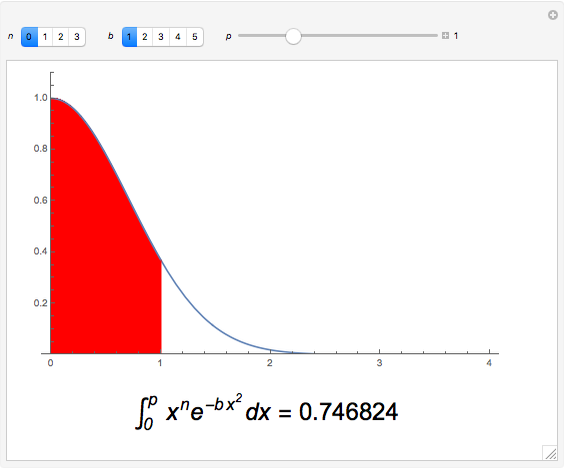
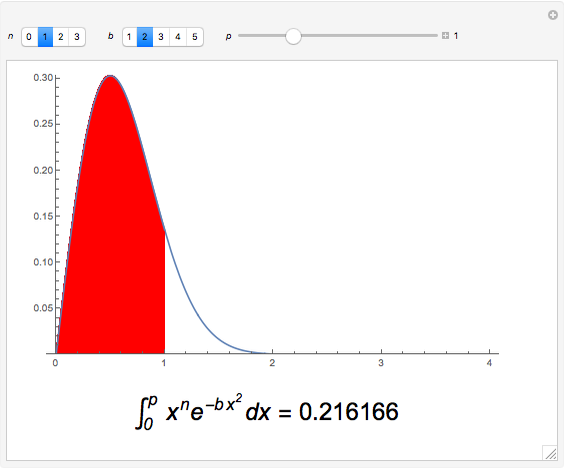
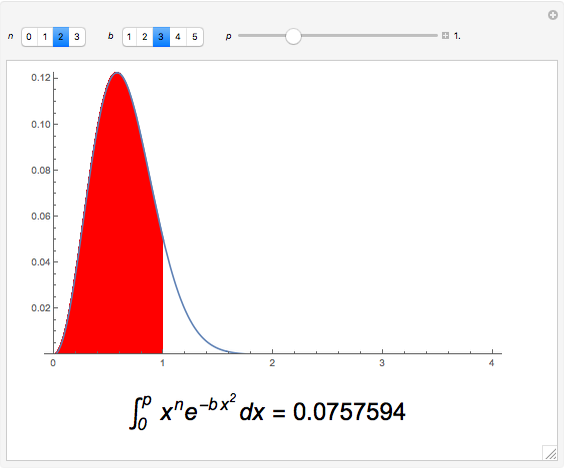
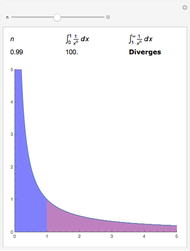
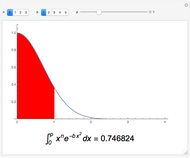
can be evaluated for positive integers  [1]. In this Demonstration, we perform numerical integrations for
[1]. In this Demonstration, we perform numerical integrations for  , with
, with  and
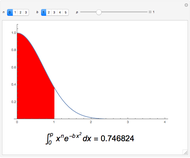
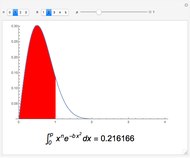
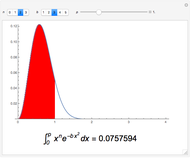
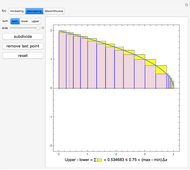
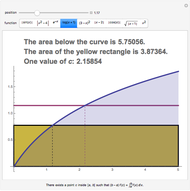
and  . The results are then represented as areas under a curve (shown in red).
. The results are then represented as areas under a curve (shown in red).
Contributed by: Casimir Kothari (January 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] E. W. Weisstein, "Gaussian Integral," Wolfram MathWorld. (Jan 25, 2016) mathworld.wolfram.com/GaussianIntegral.html (Wolfram MathWorld).
Permanent Citation
"Some Gaussian Integrals"
http://demonstrations.wolfram.com/SomeGaussianIntegrals/
Wolfram Demonstrations Project
Published: January 26 2016