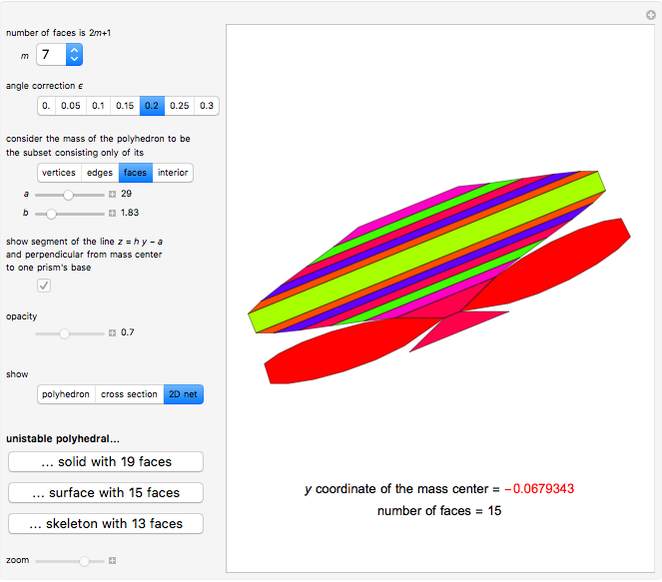
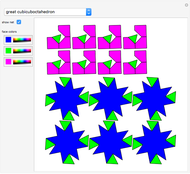
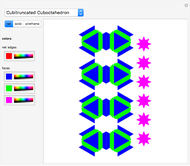
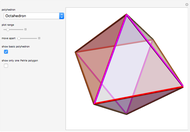
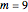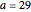A polyhedral solid with uniform density is unistable (or monostable) if it is stable on exactly one face. Besides these polyhedra, this Demonstration also considers polyhedra as surfaces, skeletons, and as a set of vertices.
[more]
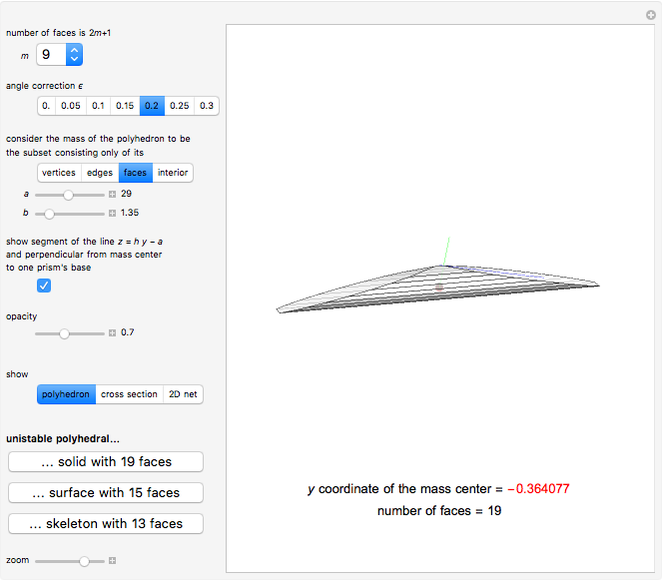
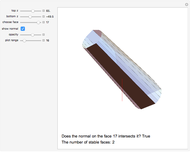
In 1968, Guy constructed a unistable polyhedron with 19 faces. It is a kind of truncated prism. Half of its cross section consists of 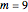 right-angled triangles (see cross section); each of the angles at the coordinate center equals
right-angled triangles (see cross section); each of the angles at the coordinate center equals  . The construction here allows the first and the last angle to be a little larger, namely
. The construction here allows the first and the last angle to be a little larger, namely  (
( is called the angle correction), and the others to be a bit smaller. If truncation makes the center of mass fall below the coordinate origin, only the bottom face (see cross section) and possibly two truncated bases are stable. But the last two can be made unstable by making the length
is called the angle correction), and the others to be a bit smaller. If truncation makes the center of mass fall below the coordinate origin, only the bottom face (see cross section) and possibly two truncated bases are stable. But the last two can be made unstable by making the length  of the shortest lateral edge be sufficiently large. In this case, the perpendicular from the center of mass (green line) to the corresponding prism's new basis must not intersect it. So the blue line on the basis and the green line must meet outside of the solid.
of the shortest lateral edge be sufficiently large. In this case, the perpendicular from the center of mass (green line) to the corresponding prism's new basis must not intersect it. So the blue line on the basis and the green line must meet outside of the solid.
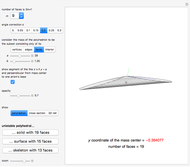
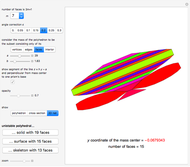
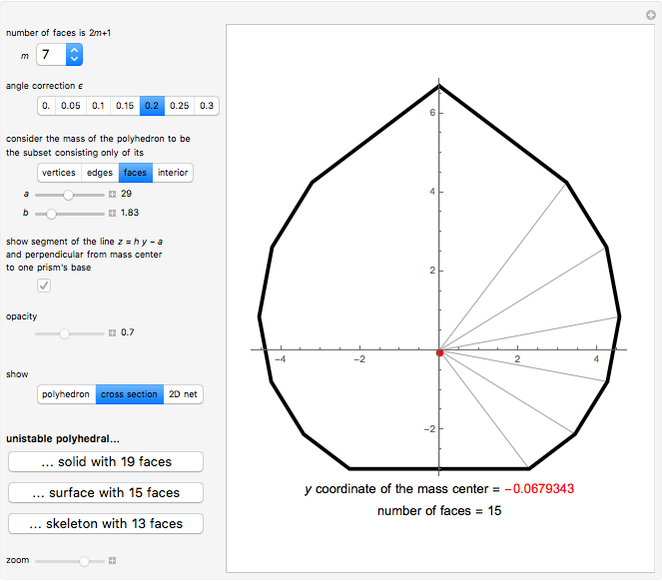
For example, to find a unistable polyhedral surface with 15 faces, choose  , consider the polyhedron as a set of faces, and set
, consider the polyhedron as a set of faces, and set 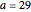 ,
,  . To get a unistable polyhedron, its center of mass (red point) must be below the origin (black point). The meaning of the parameters
. To get a unistable polyhedron, its center of mass (red point) must be below the origin (black point). The meaning of the parameters  is:
is:  , which are the
, which are the  coordinates of intersections of the polyhedron with the
coordinates of intersections of the polyhedron with the  axis. So the slope of the blue line is
axis. So the slope of the blue line is  , where
, where  is the distance of the origin to the shortest lateral edge of the polyhedron.
is the distance of the origin to the shortest lateral edge of the polyhedron.
[less]
Details
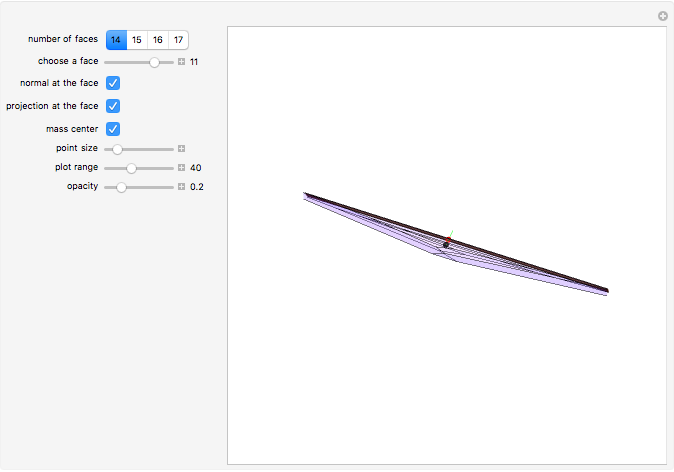
A face of a polyhedron is stable if and only if the orthogonal projection of the center of mass onto the face lies inside the face or on the edge [1, p. 273].
References
[1] J. Bryant and C. Sangwin, How Round Is Your Circle?: Where Engineering and Mathematics Meet, Princeton: Princeton University Press, 2008 pp. 273–276.
[2] R. K. Guy, A Unistable Polyhedron, Calgary: University of Calgary Department of Mathematics, 1968.
[3] J. H. Conway, M. Goldberg, and R. K. Guy, Problem 66-12, SIAM Review 11, 1969 pp. 78–82.