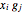Spectral Properties of Directed Cayley Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
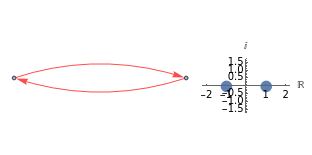
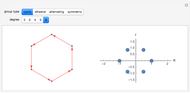
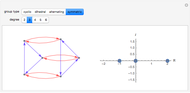
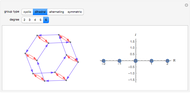
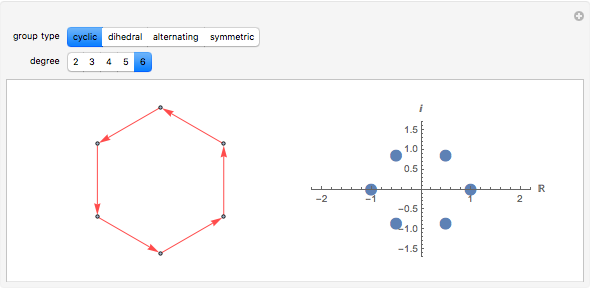
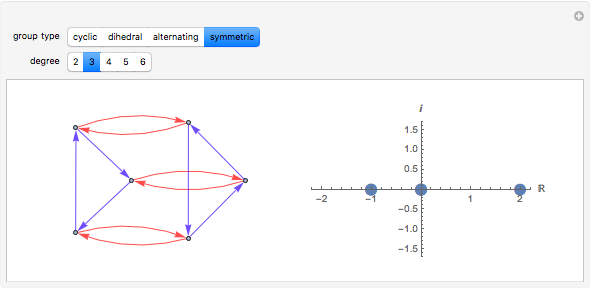
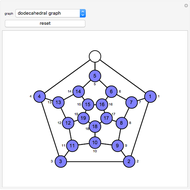
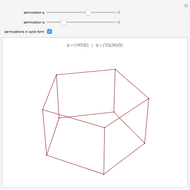
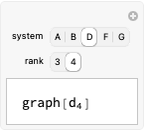
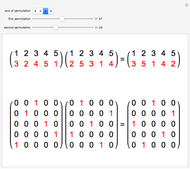
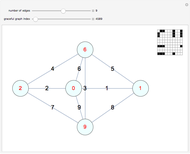
Spectral graph theory examines the structure of a graph by studying the eigenvalues of certain matrices associated with the graph. A Cayley graph is a construction that embeds the structure of a group generated by a certain generating set. Since graphs are a means to study groups, and linear algebra gives the spectral theorems to study graphs, the next logical step is to use spectral theory to examine finite groups.
[more]
Contributed by: Bill Langhoff (June 2015)
Based on a program by: Jaime Rangel-Mondragon
After work done in collaboration with: Tom Goral
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation