Sphere with Tunnel Brachistochrone

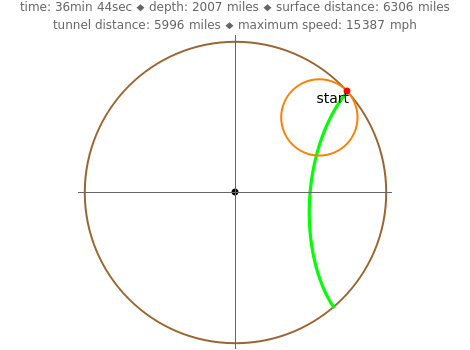
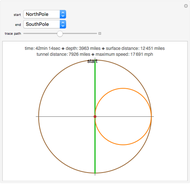
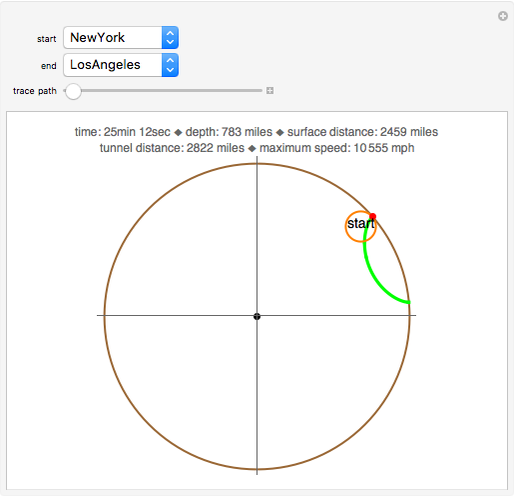
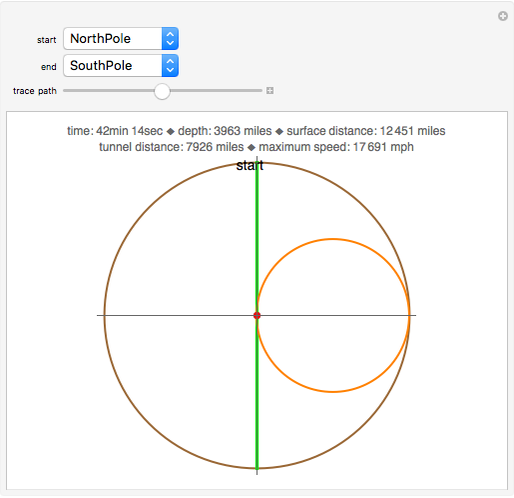
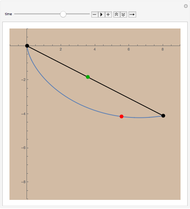
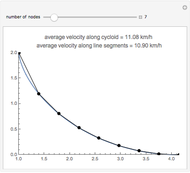
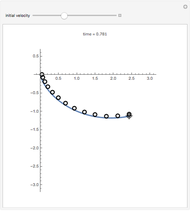
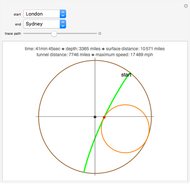
In theory, some transportation problems might be solved by digging a network of tunnels through the Earth connecting different cities (e.g., New York and Tokyo). The idea is to use the Earth's gravity as the sole source of power to accelerate a train from rest in a starting city, have it then pass through a tunnel, finally coasting to rest in the destination city. Assuming that the Earth has a uniform mass density and ignoring friction, air resistance, and the Earth's rotation, the calculus of variations shows that a hypocycloid is the shape of the tunnel required to achieve the trip between two cities in the minimum possible time. The hypocycloid is the path followed by a fixed point on a small circle rolling, without slipping, along the interior of a larger circle (i.e., the Earth). This Demonstration shows the shape of the tunnel's path as well as the travel time, distance, maximum tunnel depth, and the maximum speed of the train assuming that tunnels are dug between principal cities around the world.