Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

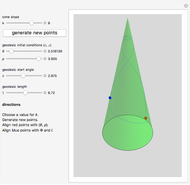
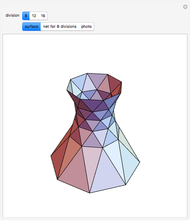
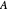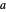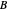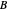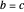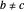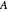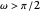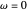Spherical Cycloids Generated by One Cone Rolling on Another

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

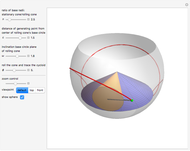
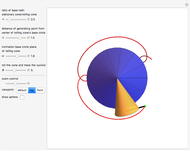
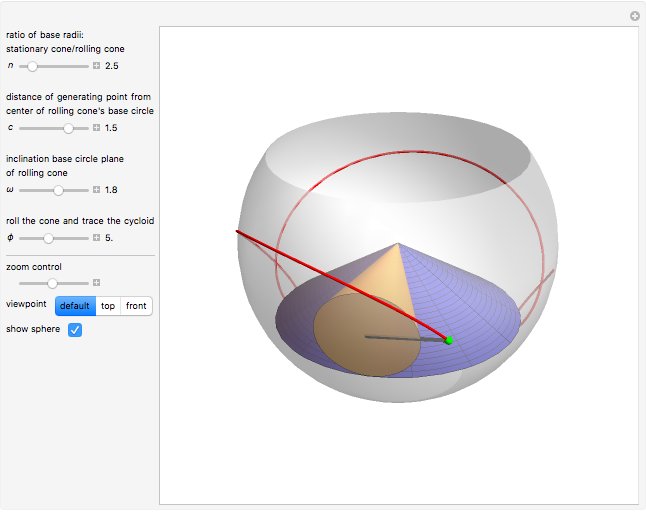
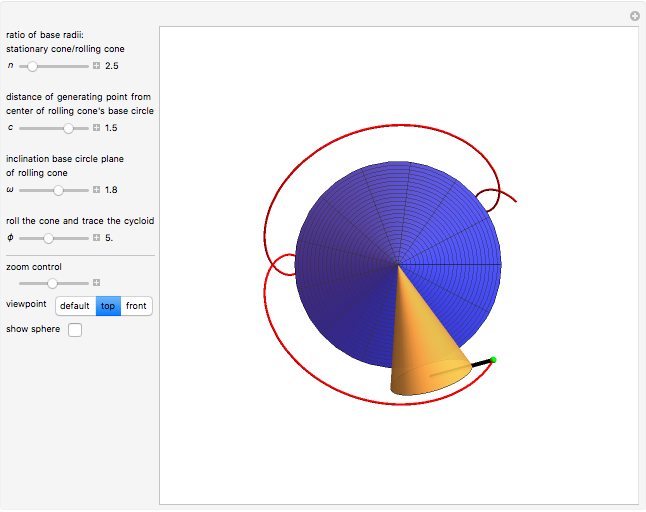
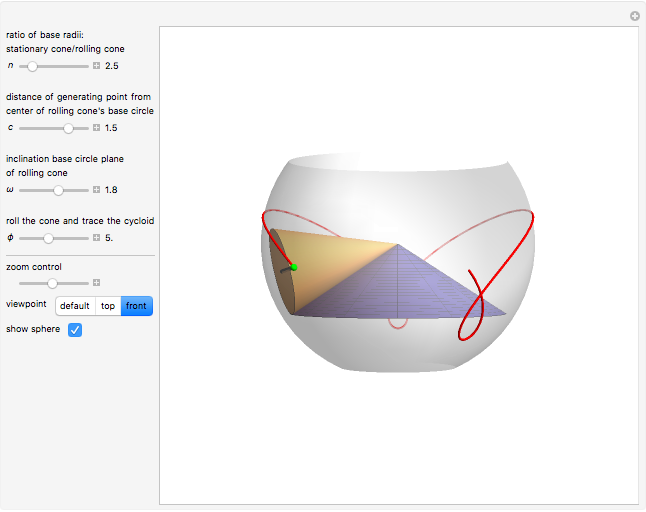
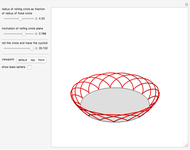
In this Demonstration, we generate a spherical trochoid with a cone that rolls without slipping on another stationary cone. The generated curve is called a spherical cycloid or spherical trochoid.

[more]

Let and be the base circles of the stationary and rolling cones, respectively, with radii and . Let be the distance of the generating point to the center of .

A spherical cycloid is traced by a point on the edge of , that is, ; a spherical trochoid is traced if .

A closed curve is obtained if is rational.

Let be the angle between the planes of and . For a spherical hypotrochoid, , and for a spherical epitrochoid, .

In the extreme cases or , we get a planar hypotrochoid or epitrochoid, respectively.

[less]

Contributed by: Erik Mahieu (December 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Let be the angular displacement of 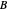along the edge of . Since 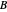rolls without sliding, its angular displacement around its center is .

The point on a copy of 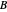centered at 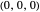in the 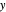- plane and at a distance from its center is:

.

First rotate this circle by 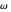around the 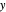axis:

.

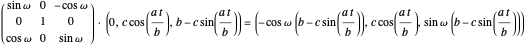Now translate the circle over a distance 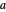along the 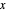axis to get:

.

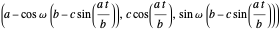Finally, rotate this circle by an angle around the axis:

.

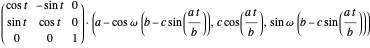This gives the parametric equation of the spherical trochoid:

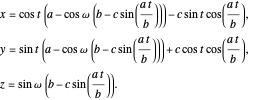
The spherical trochoid is on a sphere with center at 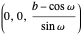and radius .

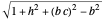Reference

[1] Kinematic Models for Design Digital Libary. "Reuleaux Collection, Cornell: Cycloid Rolling Models." (Dec 5, 2016) kmoddl.library.cornell.edu/model.php?cat=R.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send