Spherical Harmonics
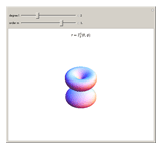
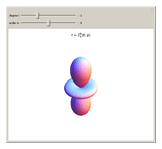
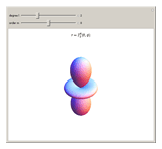
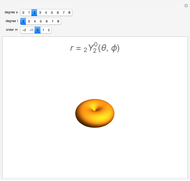
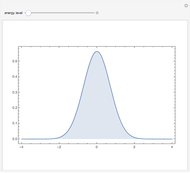
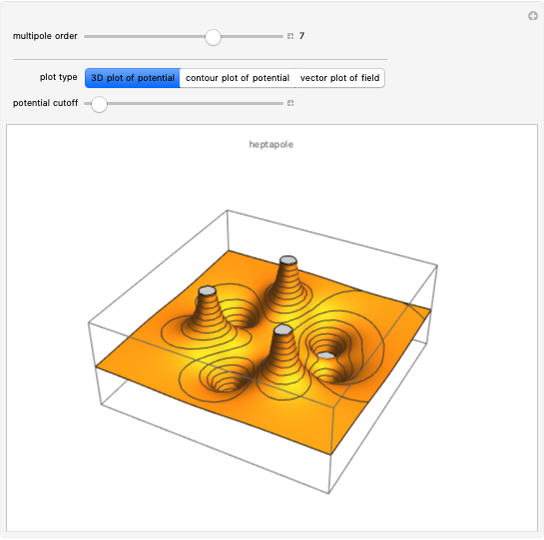
Spherical harmonics give the angular part of the solution to Laplace's equation in spherical coordinates. They arise in many practical situations, notably atomic orbitals, particle scattering processes and antenna radiation patterns.
Contributed by:
Stephen Wolfram
X
X
X
Show Source Code
|
Download Source Code Notebook
In physical settings, the degree
is normally called the
orbital quantum number
and the order
the
magnetic quantum number
.
Spherical Harmonic
(
Wolfram
MathWorld
)
"
Spherical Harmonics
" from
The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/SphericalHarmonics/
Contributed by:
Stephen Wolfram
3D Graphics
Chemistry
College Physics
Electromagnetism
Physical Chemistry
Quantum Mechanics
Quantum Physics
Special Functions
Waves
Harmonic Oscillator Eigenfunctions
Hydrogen Orbitals
Visualizing Atomic Orbitals
Nodal Surfaces of Degenerate States
Electric Dipole Potential
Harmonic Oscillator in a Half-space with a Moving Wall
Bonding and Antibonding Molecular Orbitals
Wave Functions of Identical Particles
Time-Evolution of a Wavepacket in a Square Well
Product of Two Gaussians
Make a new version of this Demonstration
Upload a new Demonstration
Contact The Wolfram Demonstrations Project Team
Site Index
Wolfram Research
© 2008
The Wolfram Demonstrations Project & Contributors
Terms of Use
Privacy Policy
RSS
Atom
