Spherical Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
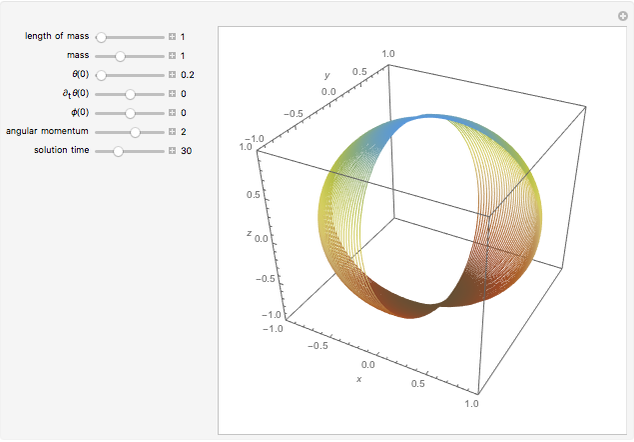
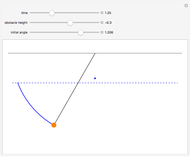
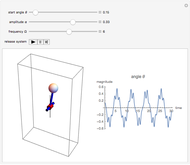
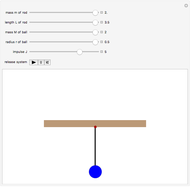
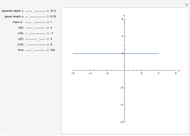
The top of a pendulum of length  hangs from the origin. The mass
hangs from the origin. The mass  at the bottom end of the pendulum has coordinates
at the bottom end of the pendulum has coordinates  ,
,  ,
,  , where the vector
, where the vector  from the origin to
from the origin to  is at an angle θ to the negative
is at an angle θ to the negative  axis. The spherical coordinates of
axis. The spherical coordinates of  are (
are ( ,
,  ,
,  ) with
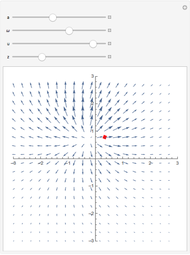
) with  . The Lagrange function and equations give
. The Lagrange function and equations give  ,
,  , and
, and  . The integration constants are
. The integration constants are  ,
,  ,
,  , and the angular momentum
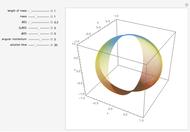
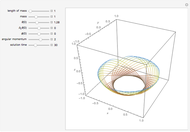
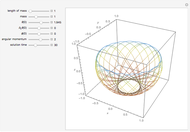
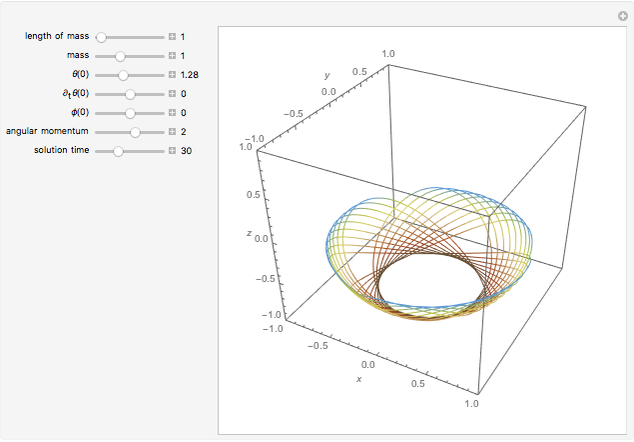
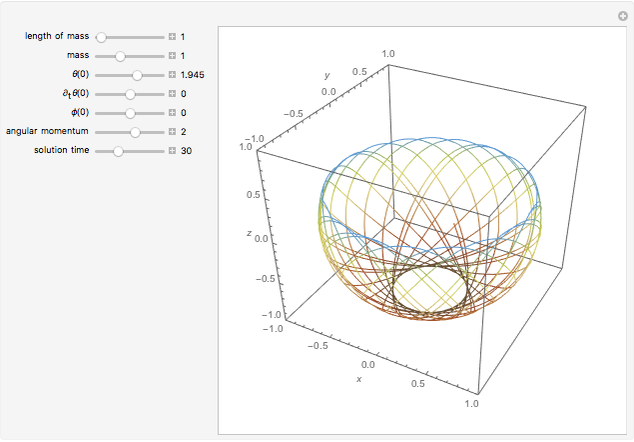
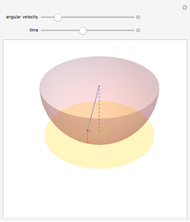
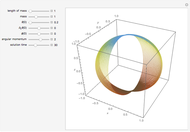
, and the angular momentum  . The movement of the spherical pendulum is constrained to the spherical shell between
. The movement of the spherical pendulum is constrained to the spherical shell between  and
and  for all
for all  values. The pendulum cannot reach the singular points
values. The pendulum cannot reach the singular points  and
and  for
for  . When the angular momentum vanishes, the pendulum moves in a plane.
. When the angular momentum vanishes, the pendulum moves in a plane.
Contributed by: Franz Krafft (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Spherical Pendulum"
http://demonstrations.wolfram.com/SphericalPendulum/
Wolfram Demonstrations Project
Published: March 7 2011