Spherical Pythagorean Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
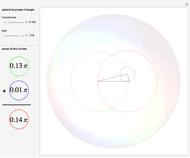
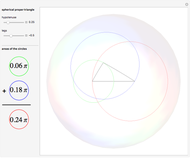
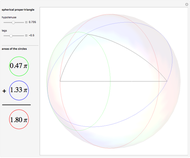
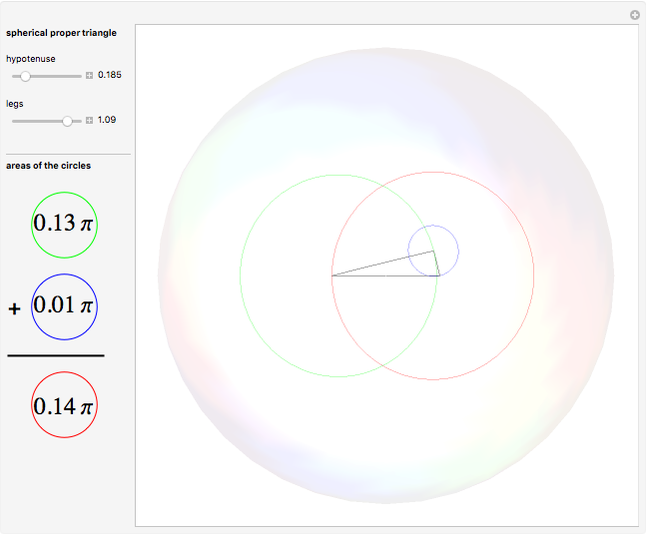
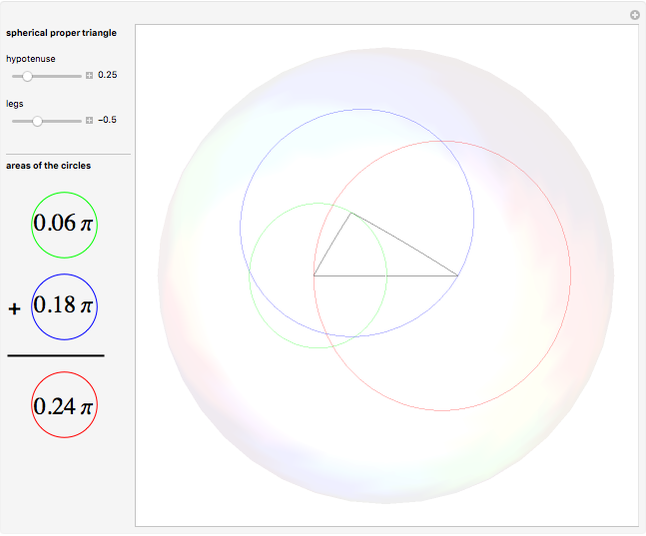
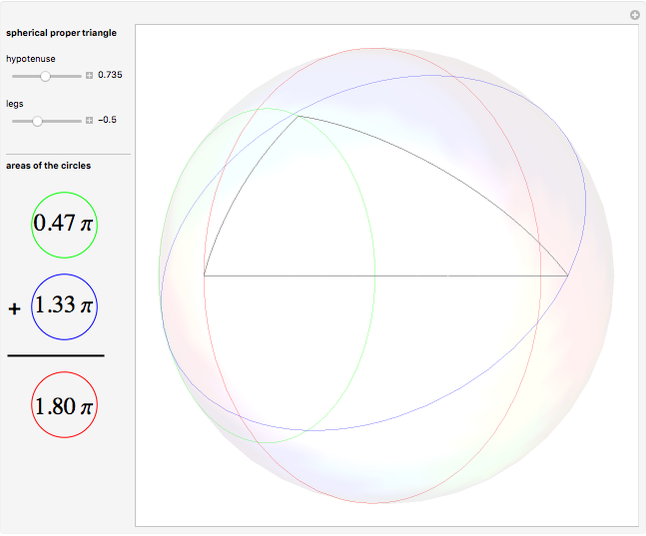
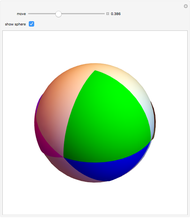
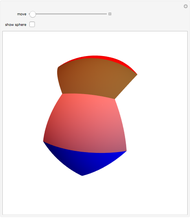
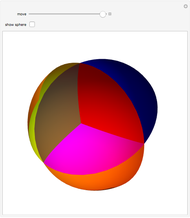
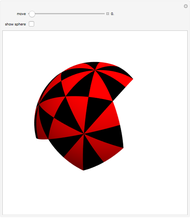
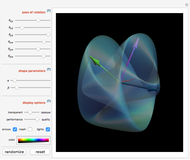
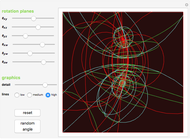
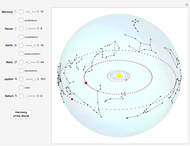
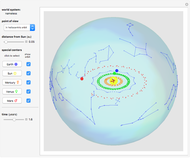
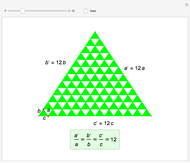
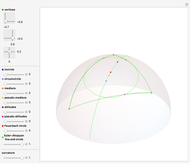
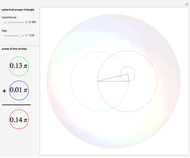
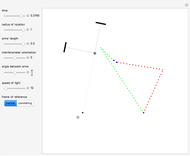
Define a "proper triangle" as a triangle having one angle equal to half the sum of its three interior angles. Call that angle the "proper angle," the side opposite to it the "hypotenuse," and the other two sides the "legs." In Euclidean geometry, the class of proper triangles corresponds to right triangles, for which the classical Pythagorean theorem holds. In spherical geometry, the theorem generalizes as follows: in proper spherical triangles (sides being arcs of great circles), the area of the circle having as radius the hypotenuse equals the sum of the areas of the circles having as radii the legs.
Contributed by: Paolo Maraner (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This form of the Pythagorean theorem was first stated and proved in the hyperbolic plane by Maria Teresa Calapso in [1]. The theorem was then independently rediscovered in [2] and [3] on the sphere (see also [4]).
References
[1] M. T. Familiari-Calapso, "Sur une classe de triangles et sur le théorème de Pythagore en géométrie hyperbolique", Comptes rendus de l'Académie des sciences Série A-B, 268, 1969 pp. A603–A604.
[2] W. Dickinson and M. Salmassi, "The Right Right Triangle on the Sphere," The College Mathematics Journal, 39(1), 2008 pp. 24–33.
[3] P. Maraner, "A Spherical Pythagorean Theorem," The Mathematical Intelligencer, 32(3), 2010 pp. 46–50. doi:10.1007/s00283-010-9152-9.
[4] V. Pambuccian, "Maria Teresa Calapso's Hyperbolic Pythagorean Theorem," The Mathematical Intelligencer, 32(4), 2010 p. 2. link.springer.com/article/10.1007%2 Fs00283-010-9169-0.
Permanent Citation
"Spherical Pythagorean Theorem"
http://demonstrations.wolfram.com/SphericalPythagoreanTheorem/
Wolfram Demonstrations Project
Published: September 29 2015