Spheroidal Foci

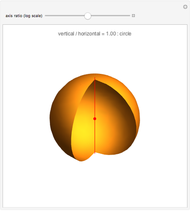
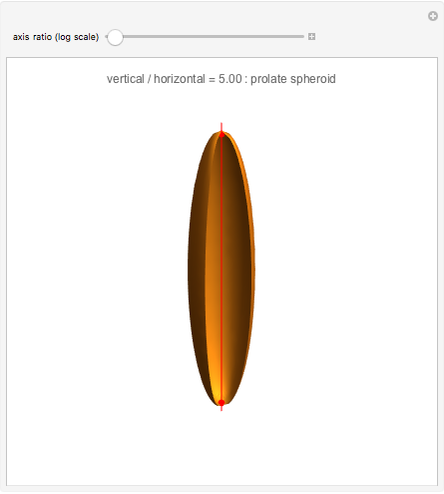
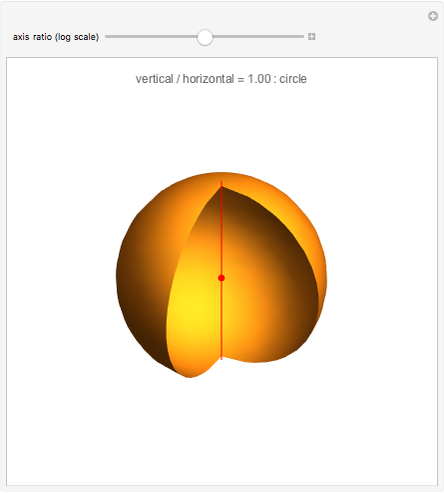
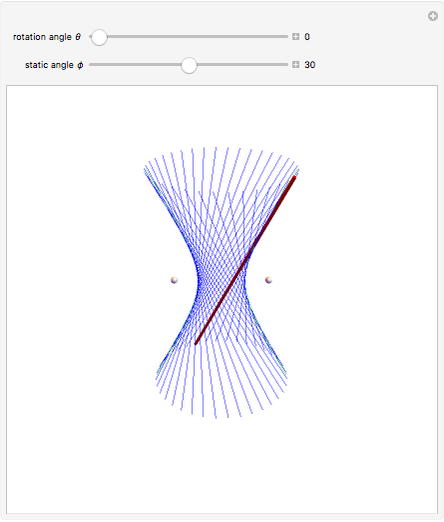
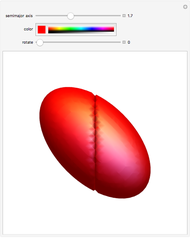
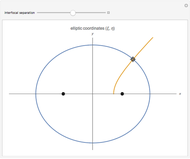
Spheroids are the surfaces of revolution of ellipses: a prolate spheroid is obtained by rotating about the major axis, while an oblate spheroid is obtained by rotating about the minor axis. When both axes are equal the spheroid becomes a sphere. In the prolate case, the foci of the ellipse are invariant under the revolution, while in the oblate they give rise to a "focal circle". This Demonstration shows how the foci vary with the shape of the spheroid.