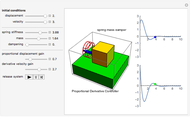
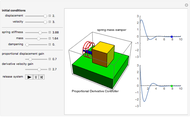
Spring-Mass-Damper (SMD) System with Proportional Derivative (PD) Controller

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
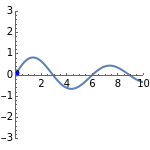
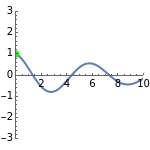
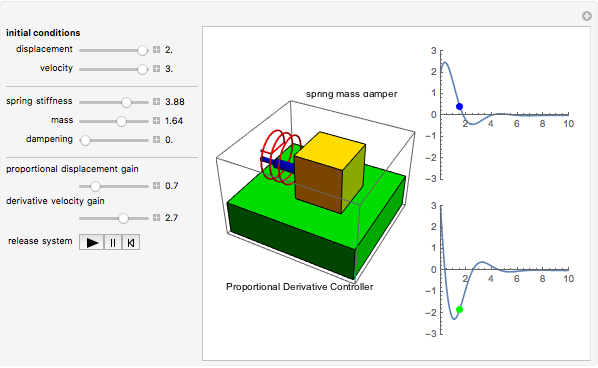
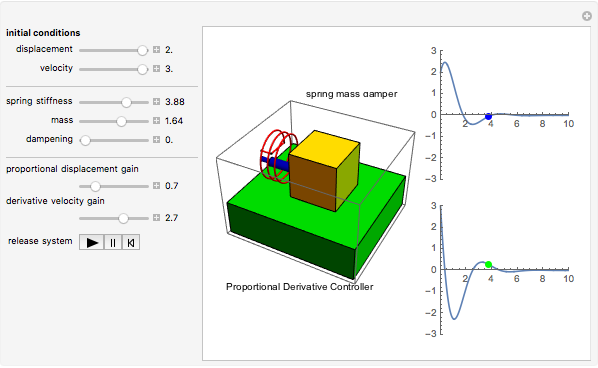
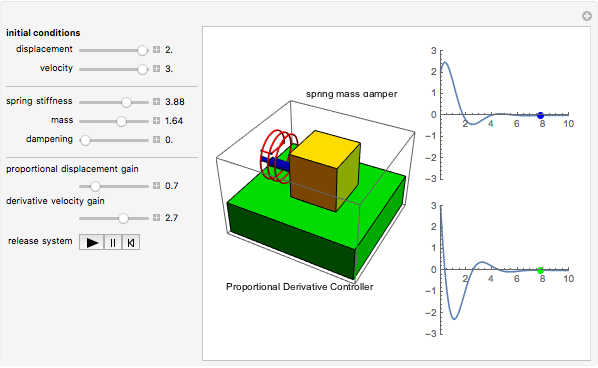
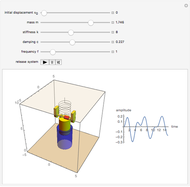
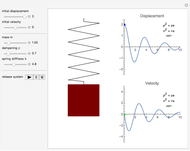
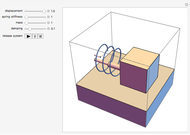
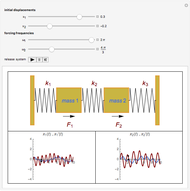
This Demonstration shows a spring-mass-damper system (SMD) with a proportional derivative (PD) controller in the time domain. The simulation includes a general solution for a free system with initial conditions (including under-, over-, and critically-damped conditions).
[more]
Contributed by: Stephen Wilkerson (Army Research Laboratory and Towson University), Nathan Slegers (University of Alabama, Huntsville), and Chris Arney (United States Military Academy, West Point) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The derivation follows the traditional form of [1] where 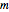 ,
,  , and
, and  are the mass, dampening coefficient, and spring’s stiffness, respectively. The variable describing the system and controller is:
are the mass, dampening coefficient, and spring’s stiffness, respectively. The variable describing the system and controller is:
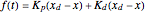
in terms of the displacement 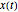 .
.
Newton’s second law leads to the differential equation:
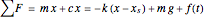 .
.
Since the stretch of the spring 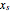 and weight of the masses
and weight of the masses 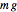 cancel,
cancel, 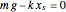 , this reduces to:
, this reduces to:
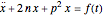 ,
,
where:
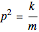
and
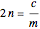 .
.
This is solved as a continuous system in the time domain. For this example it is assumed that 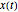 is known exactly.
is known exactly.
References: [1] W. Weaver, Jr., S. Timoshenko, and D. H. Young, Vibration Problems in Engineering, 5th ed., New York: John Wiley & Sons, 1990. [2] G. F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 4th ed., Upper Saddle River, NJ: Prentice Hall, 2002.
Permanent Citation