Square Koch Fractal Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
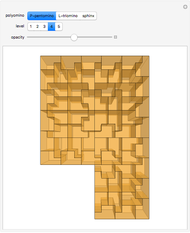
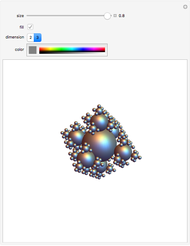
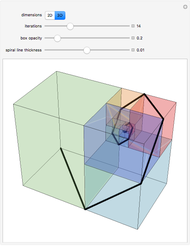
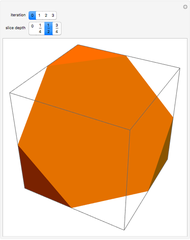
Many fractal curves can be generated using L-systems or string-rewrite rules, in which each stage of the curve is generated by replacing each line segment with multiple smaller segments in a particular arrangement. The same technique can be extended to surfaces, where each stage is constructed by replacing each square with multiple smaller squares. This Demonstration shows an analogy of the square Koch curve (Type 1) as a three-dimensional surface.
Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
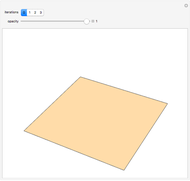
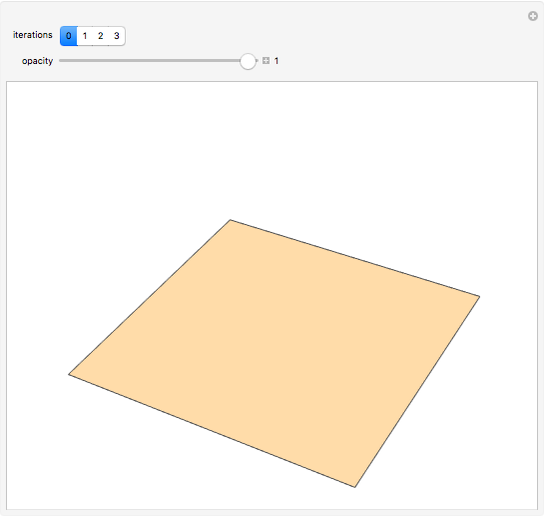
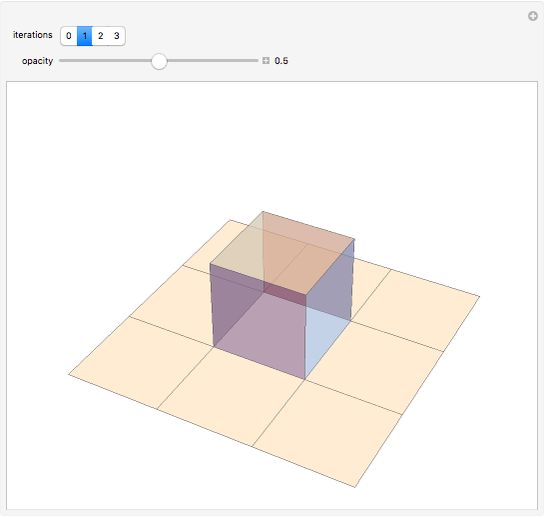
Snapshot 1: creation of the surface begins with a single square
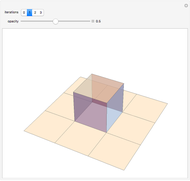
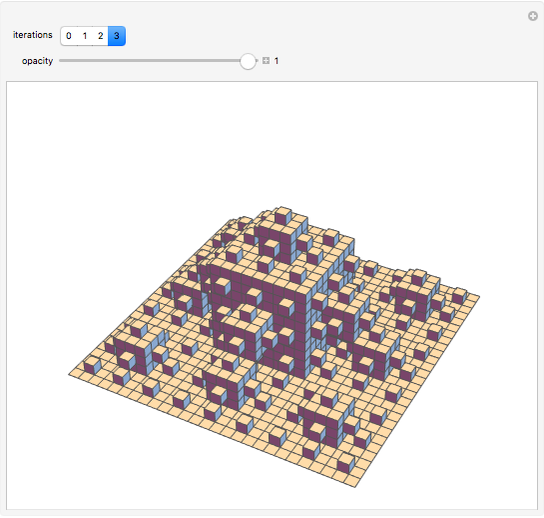
Snapshot 2: each successive iteration is created by dividing each square into nine smaller squares, "raising" the center square, and then closing the surface by adding squares that connect the raised center to the base
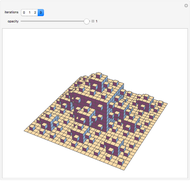
Snapshot 3: the bottom face of the surface is a Sierpinski carpet
Permanent Citation
"Square Koch Fractal Surface"
http://demonstrations.wolfram.com/SquareKochFractalSurface/
Wolfram Demonstrations Project
Published: March 7 2011