Stability and Critical Angle of a Box

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
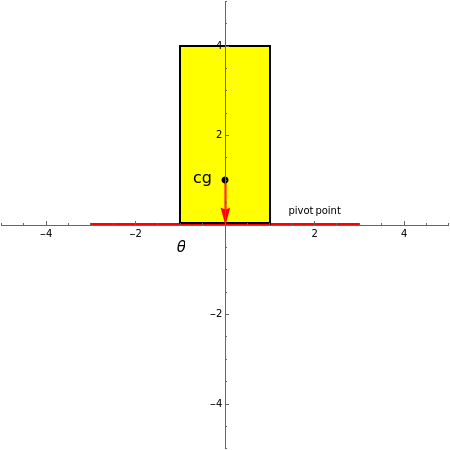
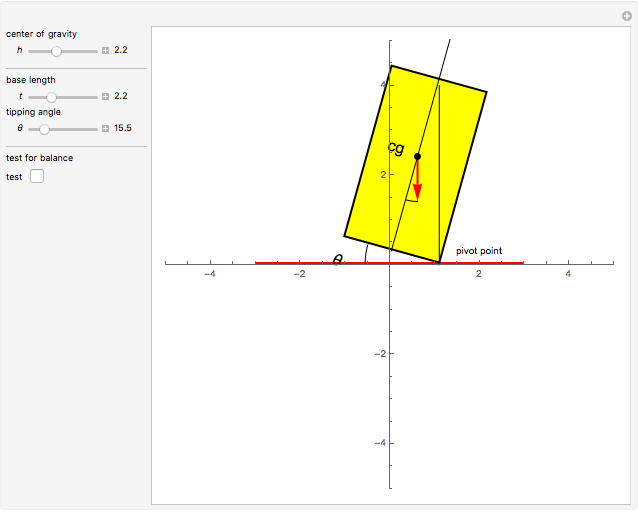
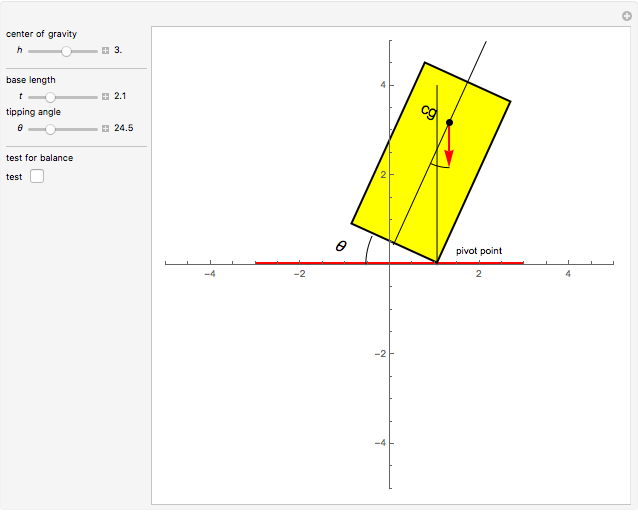
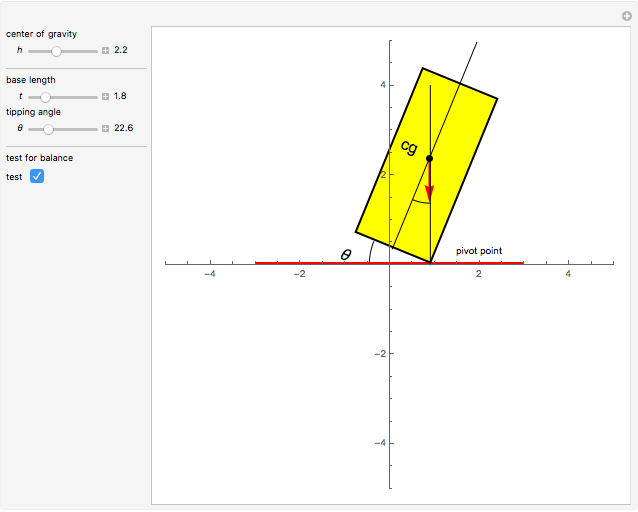
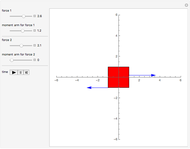
If you tilt a box, one edge of the base of support becomes a pivot point. As long as the center of gravity of the box remains over the base of support, torque due to gravity rotates the object back toward its stable equilibrium position; we say that the object is stable. But if the center of gravity moves outside the base of support, the gravitational torque causes a rotation in the opposite direction. Now the box rolls over; it is unstable. A critical angle 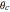 is reached when the center of gravity is directly over the pivot point. This is the point of balance, with no net torque. For vehicles, the distance between the tires—the base of support—is called the track width
is reached when the center of gravity is directly over the pivot point. This is the point of balance, with no net torque. For vehicles, the distance between the tires—the base of support—is called the track width  . If the height of the center of gravity is
. If the height of the center of gravity is  , you can see from the Demonstration that the critical angle is
, you can see from the Demonstration that the critical angle is 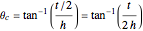 .
.
Contributed by: John Evans (September 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Stability and Critical Angle of a Box"
http://demonstrations.wolfram.com/StabilityAndCriticalAngleOfABox/
Wolfram Demonstrations Project
Published: September 18 2013