Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

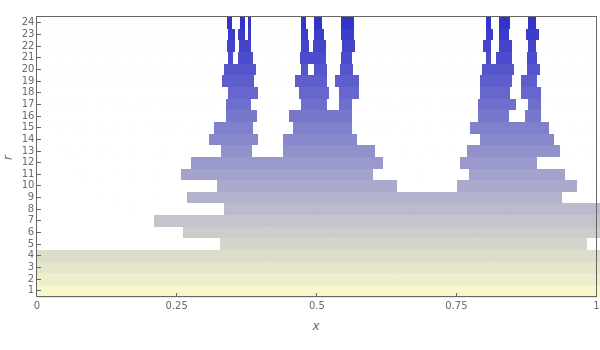
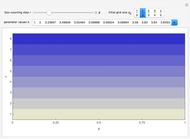
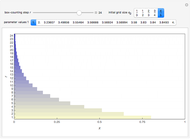
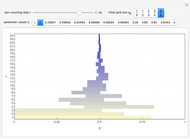
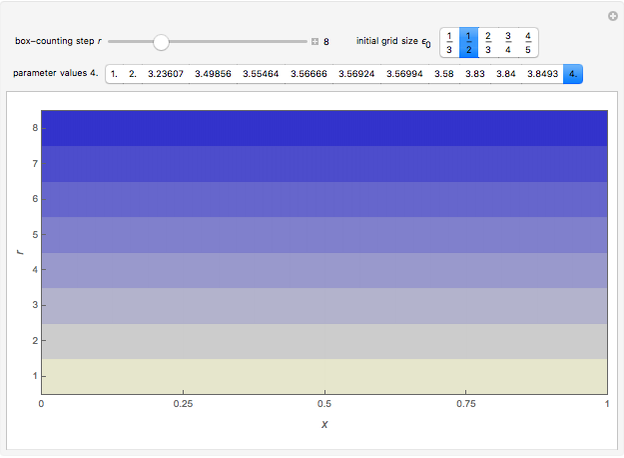
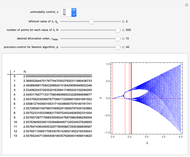
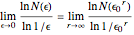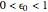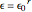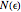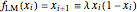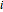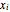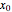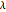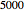Stack Diagram for 1D Box-Counting Steps

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

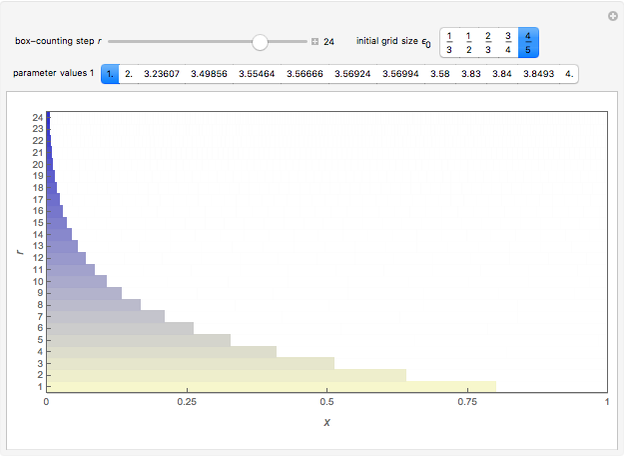
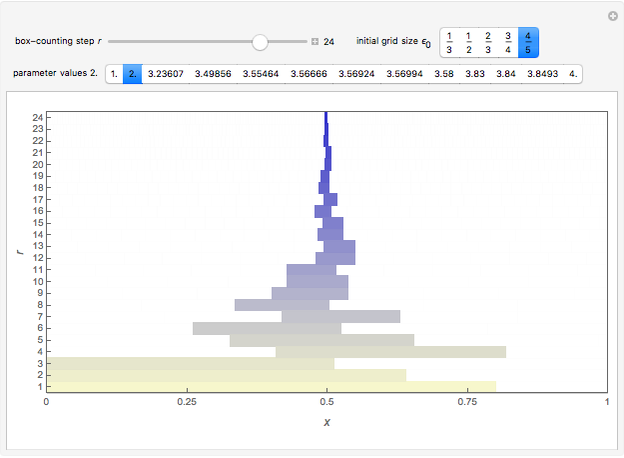
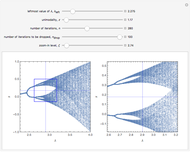
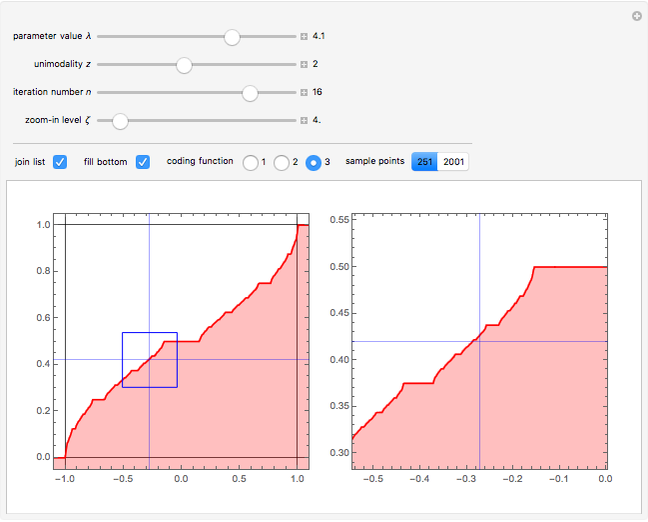
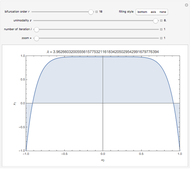
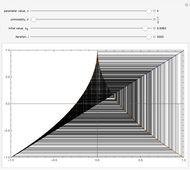
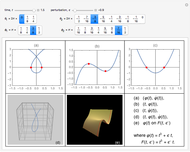
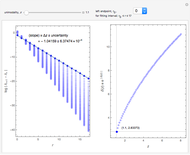
The box-counting dimension [1–4] can be defined as

[more]

,

where () is an initial box (or grid) size, is a natural number representing the box-counting step, is the box size for the scaling step, and is the number of boxes with the same size . It can be applied to any fractal, including wild fractals such as the Brownian motion. This Demonstration visualizes one-dimensional (1D) box-counting steps as a stack diagram.

The test map used in this Demonstration is the well-known logistic map [3–7] , where is an iteration number, is the iterate starting from an initial condition , and is a control parameter value; has been fixed at 5.00001, and for imitating attractors, 4000 iterates are selected from to .

[less]

Contributed by: Ki-Jung Moon (December 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

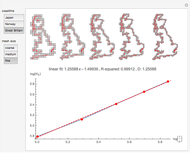
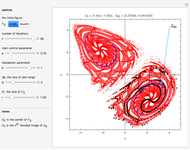
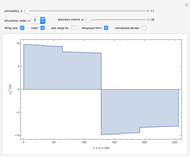
Box counting is a method of gathering data for analyzing complex patterns by breaking a dataset, object, image, etc. into smaller and smaller pieces, typically "box" shaped, and analyzing the pieces at each smaller scale [1].

References

[1] Wikipedia. "Box Counting." (Feb 1, 2013) en.wikipedia.org/wiki/Box_counting.

[2] B. Mandelbrot, The Fractal Geometry of Nature, San Francisco: W. H. Freeman, 1982.

[3] H.-O. Peitgen, H. Jürgens, and D. Saupe, Chaos and Fractals: New Frontiers of Science, 2nd ed., New York: Springer, 2004.

[4] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.

[5] R. May, "Simple Mathematical Models with Very Complicated Dynamics," Nature, 261(5560), 1976 pp. 459–467.

[6] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.

[7] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author

    Related Topics

Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send