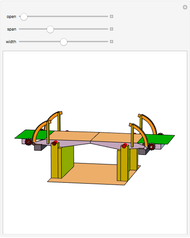
Static Deformations of Timoshenko Beams

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
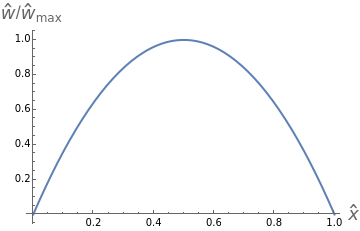
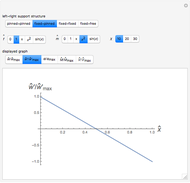
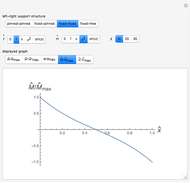
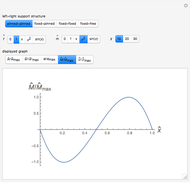
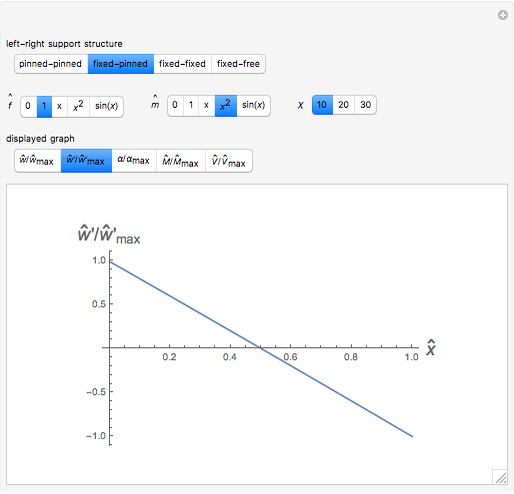
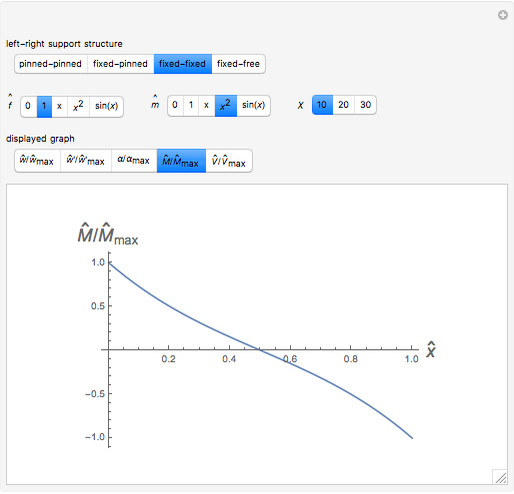
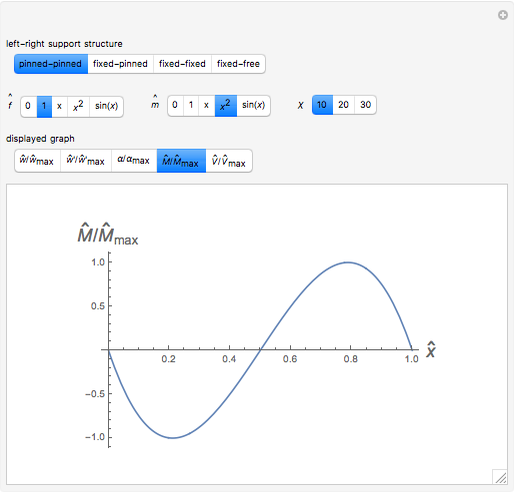
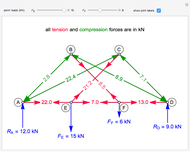
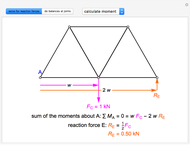
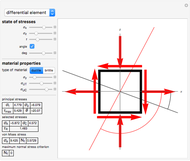
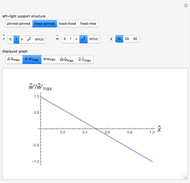
This Demonstration shows some results of the Timoshenko beam theory: the deformation 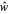 and slope
and slope 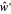 of the centerline of a beam; the angular displacement
of the centerline of a beam; the angular displacement  of its cross sections; the internal moments
of its cross sections; the internal moments  and shear
and shear 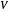 across the length of the beam with respect to specified load and end conditions. The primary purpose of this Demonstration is to provide images of beam deformation to help students understand the predictions of beam theory.
across the length of the beam with respect to specified load and end conditions. The primary purpose of this Demonstration is to provide images of beam deformation to help students understand the predictions of beam theory.
Contributed by: Prithvi Akella (April 2018)
With additional contributions by: Oliver O'Reilly and Evan Hemingway
Open content licensed under CC BY-NC-SA
Snapshots
Details
$FailedPermanent Citation