Static Equilibrium and Triangle of Forces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
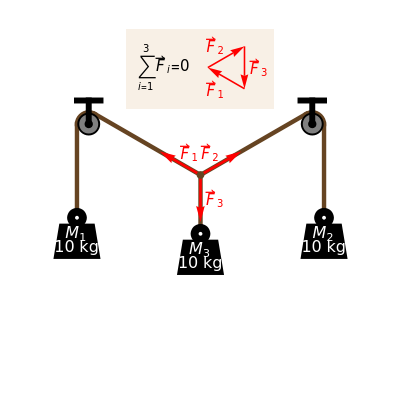
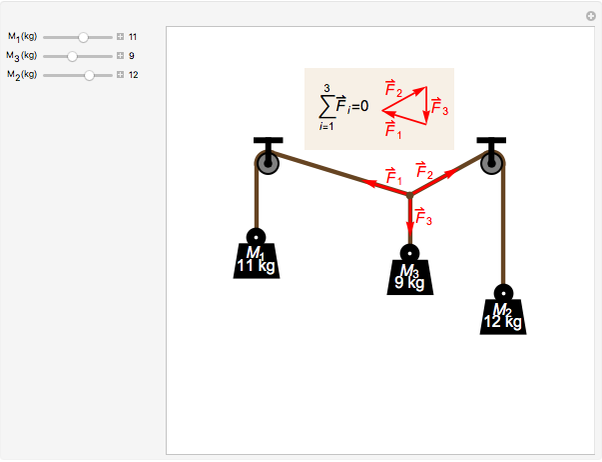
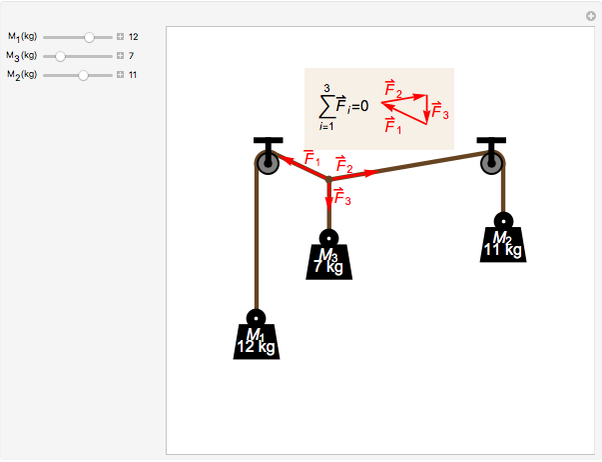
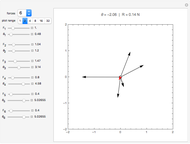
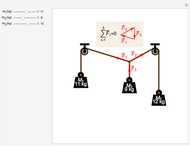
Forces are vectors, which means that they have both a magnitude and direction. To illustrate this concept, this Demonstration shows a mechanical system composed of three weights connected by strings and pulleys. The equilibrium position can be found by analyzing the forces acting on the central knot. Each force is a vector  whose norm is given by
whose norm is given by  , where
, where  is the mass attached to the string and
is the mass attached to the string and 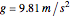 is the acceleration of gravity. According to Newton's second law, at static equilibrium the vector sum of all the forces acting on the central knot should be zero. This is illustrated in the inset by constructing a triangle of forces from the three vectors
is the acceleration of gravity. According to Newton's second law, at static equilibrium the vector sum of all the forces acting on the central knot should be zero. This is illustrated in the inset by constructing a triangle of forces from the three vectors  . You can change the magnitude of each force by changing the corresponding mass
. You can change the magnitude of each force by changing the corresponding mass  and observing how the directions of the forces adjust to maintain a triangle.
and observing how the directions of the forces adjust to maintain a triangle.
Contributed by: Gianni Di Domenico (Université de Neuchâtel) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Static equilibrium cannot be attained for every set of values of the masses  ,
,  , and
, and 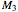 . This is related to the fact that the sides
. This is related to the fact that the sides  ,
,  ,
,  of a triangle must satisfy the triangle inequality
of a triangle must satisfy the triangle inequality  . In practice, even more stringent limits must be put on the values of the masses to avoid any accident like the central knot passing over the pulleys, or the weight
. In practice, even more stringent limits must be put on the values of the masses to avoid any accident like the central knot passing over the pulleys, or the weight 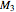 falling below the visible area. In this Demonstration, the masses
falling below the visible area. In this Demonstration, the masses  and
and  are restricted to avoid such an accident and automatically readjusted if necessary.
are restricted to avoid such an accident and automatically readjusted if necessary.
Permanent Citation