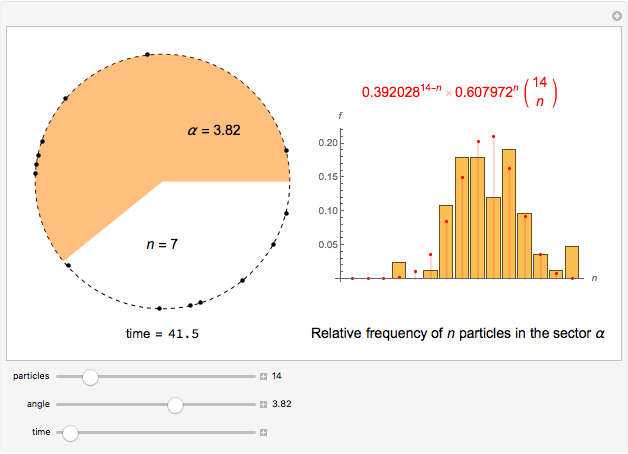
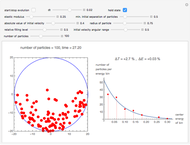
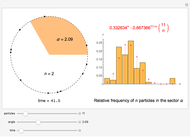
A set of independent particles in uniform rotation, but with incommensurable frequencies, has behavior similar to that of a one-dimensional perfect gas, with constant internal energy. In fact, assuming that initially the particles are at the same point on the circle, they will quickly move to positions that are distributed with a uniform density. To verify this, we choose particles and randomly assign them frequencies within a certain range. Then we compute how many particles are located within a predetermined arc of our choice at each time step. Experimentally, we verify that the distribution of the points in the arc is very well approximated by the binomial distribution 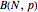, which is characterized by the total number of particles 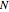and the parameter 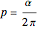. The probability that all particles return to a configuration arbitrarily close to the initial one is equal to , which is negligible, if it is even possible (a Poincare's recurrence). For example, for frequencies between about and Hz, 15 particles may return to an arc of angle 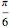around the initial position in a time of the order of the age of the universe, 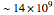years. In this Demonstration, you can observe density fluctuations in both space and time.