Steady-State 1D Conduction through a Composite Wall

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
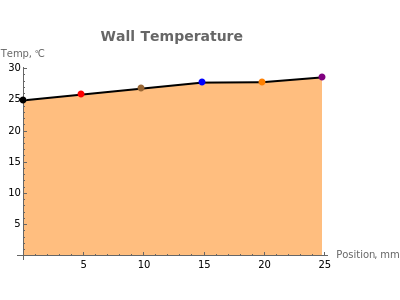
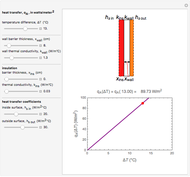
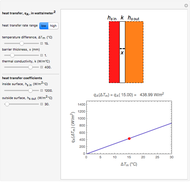
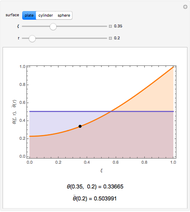
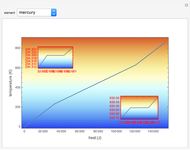
The purpose of this Demonstration is to illustrate the relationship between heat transfer and thermal conductivity  of a material by applying Fourier's law,
of a material by applying Fourier's law,  , to plot the temperature
, to plot the temperature  versus the position
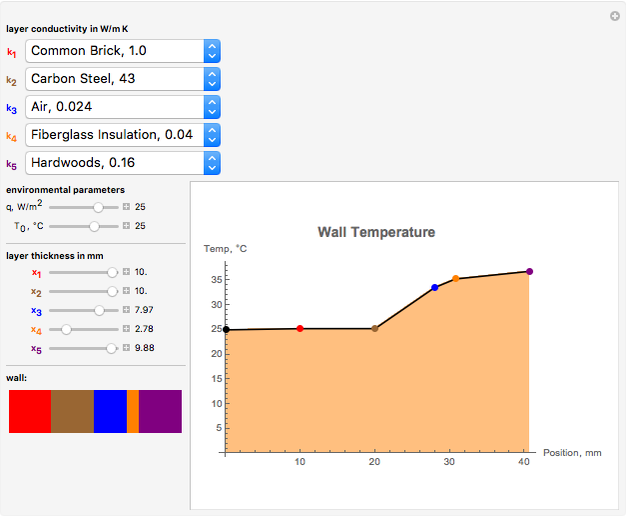
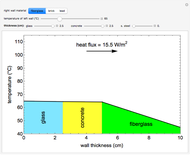
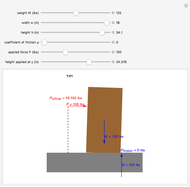
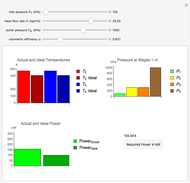
versus the position  through the depth of a multilayer wall. You can vary the total heat surface heat flux
through the depth of a multilayer wall. You can vary the total heat surface heat flux  conducted through the multilayer wall and the surface temperature at the far left side of the wall,
conducted through the multilayer wall and the surface temperature at the far left side of the wall,  . The wall has a constant cross-sectional area
. The wall has a constant cross-sectional area  in square meters in the
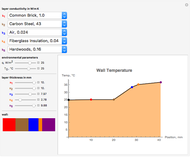
in square meters in the  direction. You can select different materials and their thicknesses for five layers of the wall, denoting
direction. You can select different materials and their thicknesses for five layers of the wall, denoting  as the thermal conductivity of layer
as the thermal conductivity of layer  . Given this information, it is possible to determine the temperature profile through the wall, showing the interior temperature at each location.
. Given this information, it is possible to determine the temperature profile through the wall, showing the interior temperature at each location.
Contributed by: Sara McCaslin and Fredericka Brown (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If  is the thermal conductivity of layer
is the thermal conductivity of layer  in W/m K and
in W/m K and  is the thickness of layer
is the thickness of layer  in m,
in m,  .
.
This Demonstration can investigate the following questions:
If you use a negative value for heat flow, do you expect the temperature on the far side of the wall to be warmer or cooler than  ?
?
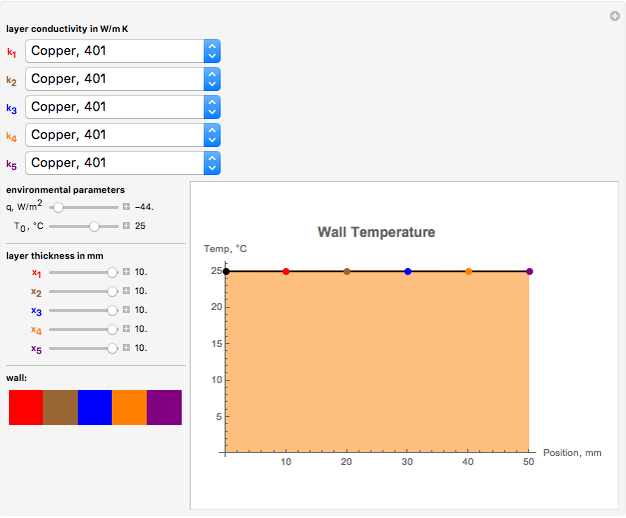
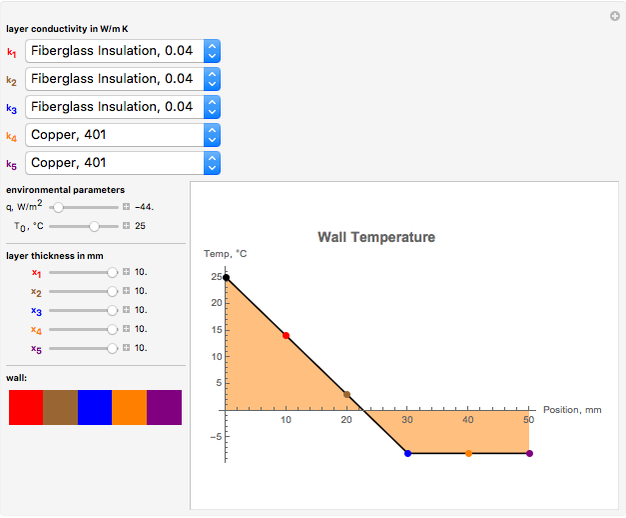
Can you verify that steel or copper does not work well as an insulating material?
Do insulating materials have a steep slope on the temperature versus position plot?
What materials make good insulators?
What materials make good conductors?
By changing  , flow rate
, flow rate  , and material types/thicknesses you can find the answers to these questions.
, and material types/thicknesses you can find the answers to these questions.
For more information on conduction through a multilayer isothermal wall, see Engineer's Edge.
Reference
[1] D. Pitts and L. E. Sissom, Schaum's Outline of Heat Transfer, New York: McGraw Hill, 1998.
Permanent Citation