Steering Multiple Radio Control (RC) Cars with One Joystick

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
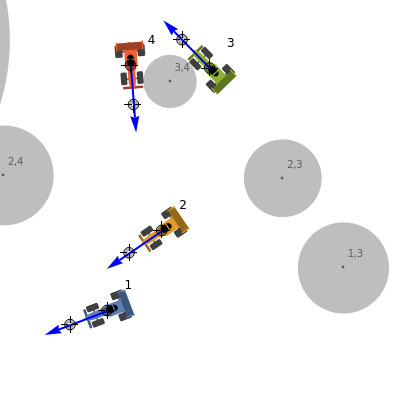
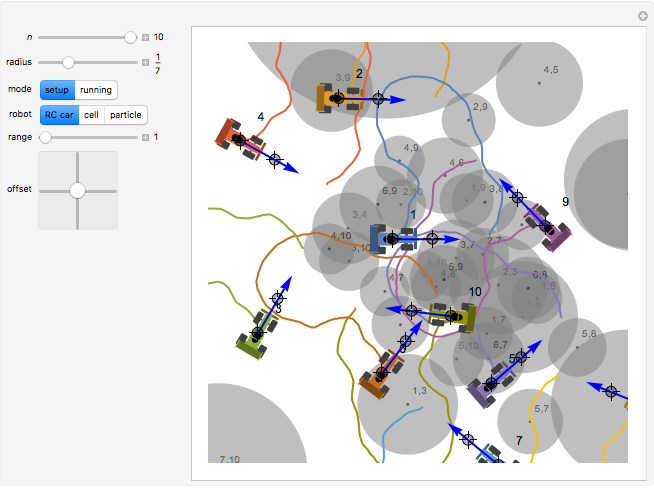
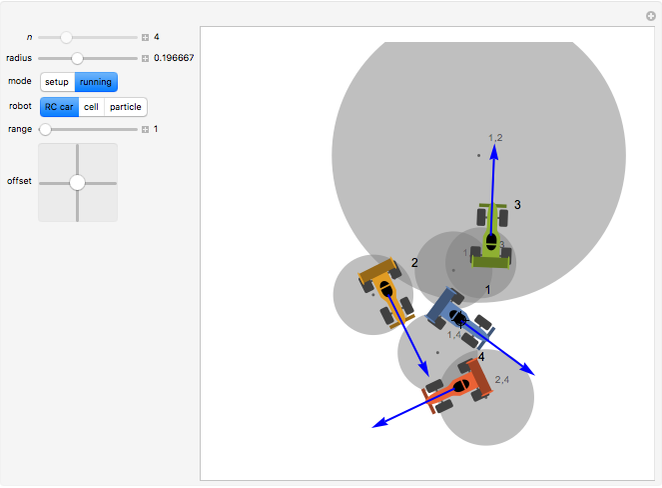
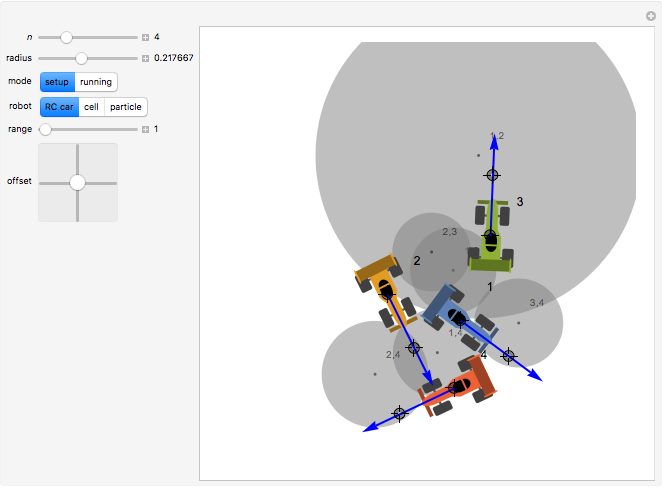
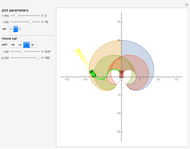
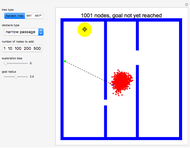
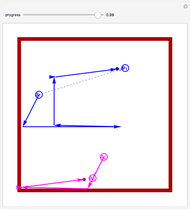
Imagine  radio control (RC) cars all controlled using the same radio frequency. When you command one car to move along a certain trajectory, all other cars follow a trajectory of the same shape, starting from their initial positions and rotated according to their initial heading. Each pair of cars can collide only in the regions shown by gray disks. During "setup," gray disks determine where two cars can collide. This collision area is a function of the position and orientation of the cars, so changing these changes the positions of the disks. The car used as reference for commands is car 1, so during "running" the gray disks show where car 1 must be positioned to make any two cars collide. The paths of the robots are drawn in different colors. Change
radio control (RC) cars all controlled using the same radio frequency. When you command one car to move along a certain trajectory, all other cars follow a trajectory of the same shape, starting from their initial positions and rotated according to their initial heading. Each pair of cars can collide only in the regions shown by gray disks. During "setup," gray disks determine where two cars can collide. This collision area is a function of the position and orientation of the cars, so changing these changes the positions of the disks. The car used as reference for commands is car 1, so during "running" the gray disks show where car 1 must be positioned to make any two cars collide. The paths of the robots are drawn in different colors. Change  to generate new robots.
to generate new robots.
Contributed by: Aaron T. Becker and Javier Garcia (January 2019)
Open content licensed under CC BY-NC-SA
Details
This model was explored by Bretl [1] and can be applied to many types of systems that are steered by a global field. The robots can be RC cars, living cells that orient themselves and move at an offset angle from a global magnetic field [2], or self-propelled magnetic dipoles with a catalytic cap oriented at random angles with respect to a magnetic dipole [3]. This model has special relevance at the micro- and nanoscales, where multiple similar robots can be considered. The robots are usually controlled by a global control signal such as a magnetic or electric field. In all models, each robot's pose is described by an  position and an orientation
position and an orientation  .
.
Robots  and
and  can meet at only one location called
can meet at only one location called  . This location exists if
. This location exists if  :
:
 .
.
If  , the robots can collide only if they start at the same position; they remain in collision thereafter. There are
, the robots can collide only if they start at the same position; they remain in collision thereafter. There are  potential collision areas. Each collision area is a disk centered at
potential collision areas. Each collision area is a disk centered at  with radius
with radius  , where
, where  is the radius of the robot.
is the radius of the robot.
Knowing where any two robots can meet enables determination of whether a collision-free path exists. Set the mode to "running": if there is a path between robot 1 and a goal location that does not touch any gray disks, following that path will avoid all robot collisions. The thumbnail image shows a path for robot 1 that avoids collisions with all 10 robots.
References
[1] T. Bretl, "Control of Many Agents Using Few Instructions," in Robotics: Science and Systems III (W. Burgard, O. Brock and C. Stachniss, eds.), Cambridge, MA: MIT Press, 2008 pp. 209–216. doi:10.15607/RSS.2007.III.027.
[2] A. Becker, Y. Ou, P. Kim, M. J. Kim and A. Julius, "Feedback Control of Many Magnetized: Tetrahymena Pyriformis Cells by Exploiting Phase Inhomogeneity," in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, IEEE, 2013 pp. 3317–3323. doi:10.1109/IROS.2013.6696828.
[3] S. Das, E. B. Steager, K. J. Stebe and V. Kumar, "Simultaneous Control of Spherical Microrobots Using Catalytic and Magnetic Actuation," in 2017 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Montreal, QC, Canada, IEEE, 2017 pp. 1–6. doi:10.1109/MARSS.2017.8001924.
Snapshots
Permanent Citation